#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#define EDGE_MAX_SIZE 100
typedef struct _EDGE_ {
int node1;
int node2;
int distance;
}EDGE;
int Edge(EDGE* graph, int x, int y, int d) {
static int i = 0;
graph[i].node1 = x;
graph[i].node2 = y;
graph[i].distance = d;
i++;
}
void Sort(EDGE* graph, int size) {
int i,j;
for (i = 1; i < size; i++) {
EDGE key = graph[i];
for (j = i - 1; j >= 0 && graph[j].distance>key.distance; j--) {
graph[j + 1] = graph[j];
}
graph[j + 1] = key;
}
}
void Print(EDGE* graph, int size) {
for (int i = 0; i < size; i++) {
printf("(node1:%d, node2:%d, distance:%d)\n",graph[i].node1, graph[i].node2,graph[i].distance);
}
}
int getParent(int* parent, int x) {
if (parent[x] == x) {
return x;
}
else {
getParent(parent, parent[x]);
}
}
void UnionParent(int* parent, int x, int y) {
x = getParent(parent, x);
y = getParent(parent, y);
if (x < y) {
parent[y] = x;
}
else {
parent[x] = y;
}
}
int find(int* parent, int x, int y) {
x = getParent(parent, x);
y = getParent(parent, y);
if (x == y) {
return 1;
}
else {
return 0;
}
}
int Kruskal(int* parent, EDGE* graph, int size) {
int cost = 0;
for (int i = 0; i < size; i++) {
int x = graph[i].node1;
int y = graph[i].node2;
if (find(parent, x, y) == 1) {
continue;
}
else {
cost += graph[i].distance;
UnionParent(parent, x, y);
printf("\n%d와 %d 연결", x, y);
}
}
return cost;
}
int main() {
EDGE* graph = (EDGE*)calloc(EDGE_MAX_SIZE, sizeof(EDGE));
assert(graph != NULL);
int* parent = NULL;
Edge(graph, 1, 7, 12);
Edge(graph, 1, 4, 28);
Edge(graph, 1, 2, 67);
Edge(graph, 1, 5, 17);
Edge(graph, 2, 4, 24);
Edge(graph, 2, 5, 62);
Edge(graph, 3, 5, 20);
Edge(graph, 3, 6, 37);
Edge(graph, 4, 7, 13);
Edge(graph, 5, 6, 45);
int edgesize = Edge(graph, 5, 7, 73); //간선의 갯수
graph = (EDGE*)realloc(graph, edgesize * sizeof(EDGE));
assert(graph != NULL);
parent = (int*)calloc(edgesize+1, sizeof(int));
assert(parent != NULL);
for (int i = 1; i <= edgesize; i++) {
parent[i] = i;
}
Sort(graph, edgesize);
printf("\n정렬결과:\n");
Print(graph, edgesize);
int cost = Kruskal(parent, graph, edgesize);
printf("\n해당 그래프의 최소 비용은 %d입니다\n", cost);
getchar();
return 0;
}
ver2) 퀵정렬 이용
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#define MAX_VERTEX 10
#define MAX_EDGE 100
typedef struct _EDGE_ {
int start;
int end;
int distance;
}EDGE;
typedef struct _GRAPH_ {
EDGE edges[MAX_EDGE];
int nVertex; //정점의 갯수
int nEdge; //간선의 갯수
}GRAPH;
int getParent(int* parent, int data) {
if (parent[data] == data) {
return data;
}
else {
return parent[data] = getParent(parent, parent[data]);
}
}
void Union(int* parent, int v1, int v2) {
v1 = getParent(parent, v1);
v2 = getParent(parent, v2);
if (v1 < v2) {
parent[v2] = v1;
}
else {
parent[v1] = v2;
}
}
void quick_sort(GRAPH* g, int start, int end) {
int pivot = start;
int left =pivot + 1;
int right = end;
if (start >= end) {
return;
}
while (left <= right) {
while (left <= end && g->edges[left].distance <= g->edges[pivot].distance) {
left++;
}
while (right > start && g->edges[right].distance >= g->edges[pivot].distance) {
right--;
}
if (left <= right) {
EDGE temp;
temp = g->edges[left];
g->edges[left] = g->edges[right];
g->edges[right] = temp;
}
else {
EDGE temp;
temp = g->edges[right];
g->edges[right] = g->edges[pivot];
g->edges[pivot] = temp;
}
}
quick_sort(g, start, right - 1);
quick_sort(g, right + 1, end);
}
void kruskal(GRAPH* g) {
int* parent = (int*)calloc(g->nVertex, sizeof(int));
assert(parent != NULL);
int cost = 0;
for (int i = 0; i < g->nVertex; i++) {
parent[i] = i;
}
quick_sort(g, 0, g->nEdge-1);
for (int i = 0; i < g->nEdge; i++) {
int start = g->edges[i].start;
int end = g->edges[i].end;
if (getParent(parent,start) == getParent(parent,end)) {
continue;
}
else {
Union(parent, start, end);
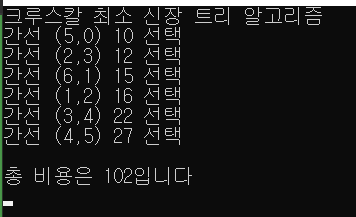
printf("간선 (%d,%d) %d 선택\n", start, end, g->edges[i].distance);
cost += g->edges[i].distance;
}
}
printf("\n총 비용은 %d입니다\n", cost);
}
void insert_edge(GRAPH* g, int start, int to, int distance) {
if (g->nEdge == MAX_EDGE - 1) {
printf("더이상 추가할 수 없습니다\n");
return;
}
g->edges[g->nEdge].start = start;
g->edges[g->nEdge].end = to;
g->edges[g->nEdge].distance = distance;
g->nEdge++;
}
int main() {
printf("크루스칼 최소 신장 트리 알고리즘\n");
GRAPH* g = (GRAPH*)calloc(1, sizeof(GRAPH));
assert(g != NULL);
insert_edge(g, 0, 1, 29);
insert_edge(g, 1, 2, 16);
insert_edge(g, 2, 3, 12);
insert_edge(g, 3, 4, 22);
insert_edge(g, 4, 5, 27);
insert_edge(g, 5, 0, 10);
insert_edge(g, 6, 1, 15);
insert_edge(g, 6, 3, 18);
insert_edge(g, 6, 4, 25);
g->nVertex = 7;
kruskal(g);
getchar();
return 0;
}
'C > 알고리즘' 카테고리의 다른 글
| Floyd Washall Algorithm(플로이드 와샬 알고리즘) (0) | 2023.08.14 |
|---|---|
| Dijkstra Algorithm[C] (0) | 2023.08.11 |
| [C] 연결리스트 큐 이용한 기수정렬 (0) | 2023.07.25 |
| 이진검색(Binary search) (0) | 2023.06.27 |
| 보초법(sentinel method) (0) | 2023.06.27 |

