위상정렬
: 순서가 정해져있는 작업을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용하는 알고리즘(=순서결정 알고리즘)
: DAG(Directed Acyclic Graph)인 경우에만 적용 가능
: 여러 개 답이 존재할 수 있음
=> 현재 그래프는 위상 정렬이 가능한지 알려줌(정렬을 다 수행하지 않았는데 공백 큐가 발생하면 위상 정렬 실패, 순환그래프)
=> 위상정렬이 가능하다면 그 결과가 무엇인지 알려줌(정렬 수행한 위상정렬 결과)
1. 동작방식
1) 진입차수가 0인 정점을 큐에 삽입
2) 큐에서 원소를 꺼내 연결된 모든 간선 제거(연결리스트 이용)
3) 간선 제거 이후 0이 된 정점들을 큐에 다시 삽입
4) 큐가 빌 때까지 2~3) 과정을 반복
-> 이때, 모든 원소를 방문하기 전 큐가 빈 경우 : 사이클 존재 (정렬 실패)
-> 모든 원소 방문 : 큐에서 꺼낸 원소 순서대로가 위상 정렬의 결과
cf> 진입차수
: 특정한 노드가 있을 때 그 노드로 들어오는 다른 노드의 갯수
2. 구현방법
스택, 큐를 이용하는 방법이 존재하는데 나는 큐 구현방식을 이용하였다
ver1)
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#define MAX_VERTEX 100
typedef struct _NODE_ {
int vertex;
struct _NODE_* link;
}NODE;
typedef struct _ADJACENT_MATRIX_ {
NODE* head[MAX_VERTEX];
int n; //정점의 개수
}ADJACENT_MATRIX;
typedef struct _QUEUE_NODE_ {
int data;
struct _QUEUE_NODE_* link;
}QUEUE_NODE;
typedef struct _QUEUE_TYPE_ {
QUEUE_NODE* front;
QUEUE_NODE* rear;
}QUEUE_TYPE;
QUEUE_TYPE* MakeQueue() {
QUEUE_TYPE* queue = NULL;
queue = (QUEUE_TYPE*)calloc(1, sizeof(QUEUE_TYPE));
assert(queue != NULL);
}
int IsEmpty(QUEUE_TYPE* q) {
return (q->front == NULL);
}
void EnQueue(QUEUE_TYPE* q, int item) {
QUEUE_NODE* newNode = NULL;
newNode = (QUEUE_NODE*)calloc(1, sizeof(QUEUE_NODE));
assert(newNode != NULL);
newNode->data = item;
newNode->link = NULL;
if (IsEmpty(q)) {
q->front = newNode;
q->rear = newNode;
}
else {
QUEUE_NODE* curNode = NULL;
curNode = q->rear;
curNode->link = newNode;
q->rear = newNode;
}
}
int DeQueue(QUEUE_TYPE* q) {
int dequeue = q->front->data;
if (IsEmpty(q)) {
fprintf(stderr, "꺼낼 노드가 존재하지 않습니다\n");
return;
}
QUEUE_NODE* curNode = q->front;
q->front = q->front->link;
free(curNode);
curNode = NULL;
return dequeue;
}
int* SetDegree(ADJACENT_MATRIX* graph) {
int* degree = NULL;
degree = (int*)calloc((graph->n) + 1, sizeof(int));
assert(degree != NULL);
for (int i = 1; i <= graph->n; i++) {
NODE* curNode = graph->head[i];
while (curNode != NULL) {
degree[curNode->vertex] += 1;
curNode = curNode->link;
}
}
printf("\n각 정점의 진입차수 배열 \n");
for (int i = 1; i <= graph->n; i++) {
printf("%d ", degree[i]);
}
printf("\n");
return degree;
}
void PrintQueue(QUEUE_TYPE* queue) {
QUEUE_NODE* curNode = queue->front;
printf("큐 출력: ");
while (curNode != NULL) {
printf("%d ", curNode->data);
curNode = curNode->link;
}
printf("\n");
}
int * Topology_sort(ADJACENT_MATRIX* graph, QUEUE_TYPE* queue) {
int* degree = SetDegree(graph);
bool* visited = (bool*)calloc((graph->n) + 1, sizeof(bool));
assert(visited != NULL);
int i;
int dequeuedata;
int* res = NULL; //큐에서 꺼낸 원소들 저장하는 배열 (위상 정렬 수행한 배열)
res = (int*)calloc(graph->n, sizeof(int));
int k = 0;
assert(res != NULL);
for (int i = 1; i <= graph->n; i++) {
for (int j = 1; j <= graph->n; j++) {
if (degree[j] == 0 && visited[j] != true) {
EnQueue(queue, j);
visited[j] = true;
}
}
PrintQueue(queue);
if (IsEmpty(queue)) {
printf("해당 그래프는 위상 정렬 알고리즘을 수행할 수 없습니다\n");
return;
}
dequeuedata = DeQueue(queue);
visited[dequeuedata] = true;
res[k++] = dequeuedata;
printf("dequeuedata: %d\n", dequeuedata);
for (int i = 0; i < graph->n; i++) {
printf("%d ", res[i]);
}
NODE* curNode = graph->head[dequeuedata];
while (curNode != NULL) {
degree[curNode->vertex] -= 1;
curNode = curNode->link;
}
printf("\n각 정점의 진입차수 배열 \n");
for (int i = 1; i <= graph->n; i++) {
printf("%d ", degree[i]);
}
printf("\n");
printf("방문 배열\n");
for (int i = 1; i <= graph->n; i++) {
printf("%d ", visited[i]);
}
printf("\n\n");
}
return res;
}
ADJACENT_MATRIX* MakeGraph() {
ADJACENT_MATRIX* graph = NULL;
graph = (ADJACENT_MATRIX*)calloc(1, sizeof(ADJACENT_MATRIX));
assert(graph != NULL);
return graph;
}
void insertVertex(int vertex, ADJACENT_MATRIX* g) {
if (g->n >= MAX_VERTEX - 1) {
fprintf(stderr, "더이상 정점을 추가하실 수 없습니다\n");
return;
}
else {
g->n++;
}
}
void insertEdge(int u, int v, ADJACENT_MATRIX* g) {
if (u > g->n || v > g->n) {
fprintf(stderr, "해당 정점은 그래프에 존재하지않습니다\n");
return;
}
else {
NODE* newNode = NULL;
newNode = (NODE*)calloc(1, sizeof(NODE));
assert(newNode != NULL);
newNode->vertex = v;
newNode->link = NULL;
NODE* curNode = g->head[u];
NODE* preNode = g->head[u];
if (g->head[u] == NULL) {
g->head[u] = newNode;
}
else {
while (curNode != NULL) {
preNode = curNode;
if (curNode->vertex > newNode->vertex) {
break;
}
curNode = curNode->link;
}
newNode->link = preNode->link;
preNode->link = newNode;
}
}
}
void PrintGraph(ADJACENT_MATRIX* graph) {
int i;
for (i = 1; i <= graph->n; i++) {
printf("[HEAD: %d] ", i);
NODE* curNode = graph->head[i];
while (curNode != NULL) {
printf("=> %d ", curNode->vertex);
curNode = curNode->link;
}
printf("\n");
}
}
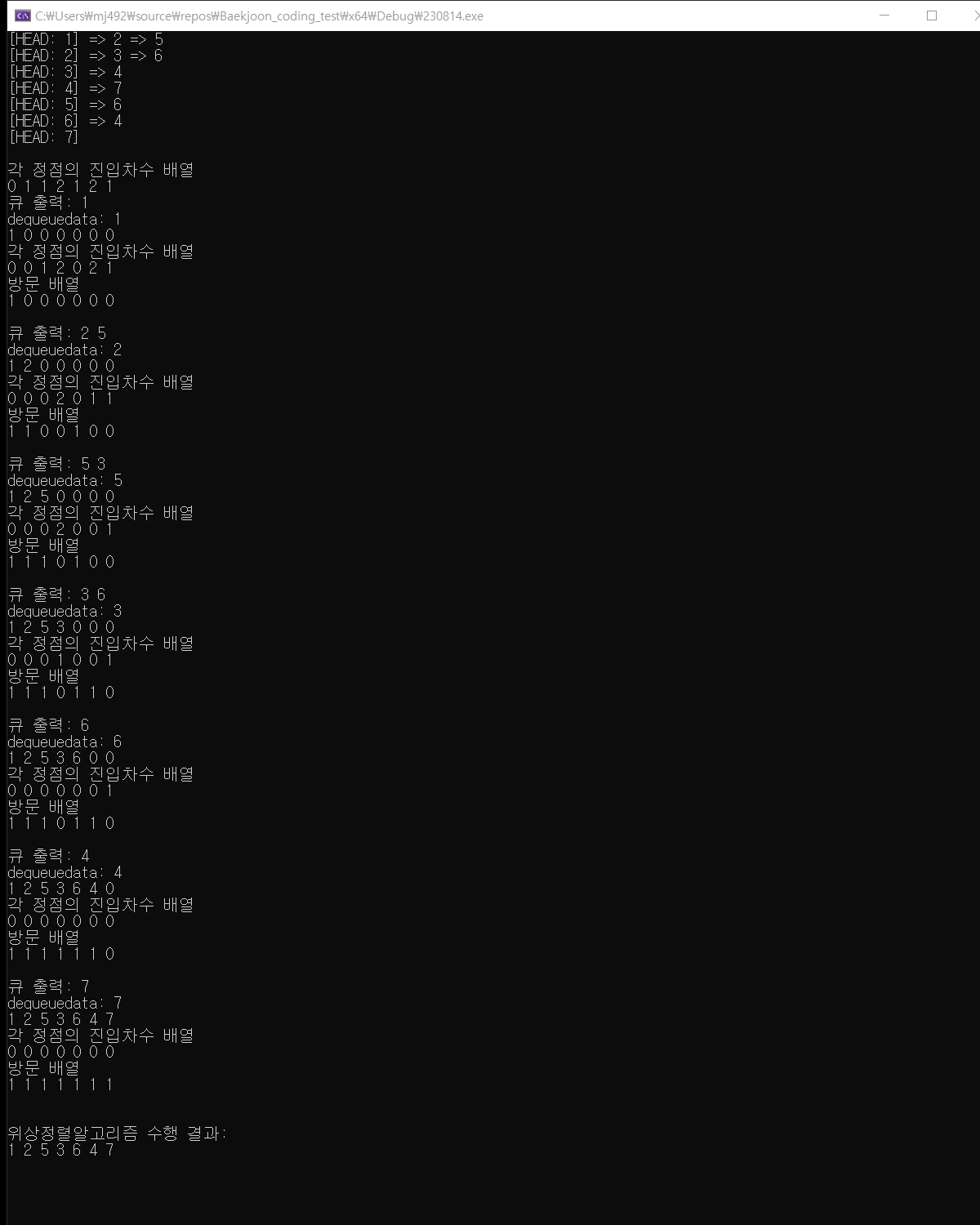
int main() {
ADJACENT_MATRIX* graph = MakeGraph();
QUEUE_TYPE* queue = MakeQueue();
for (int i = 1; i < 8; i++) {
insertVertex(i, graph);
}
insertEdge(1, 2, graph);
insertEdge(1, 5, graph);
insertEdge(2, 3, graph);
insertEdge(2, 6, graph);
insertEdge(3, 4, graph);
insertEdge(4, 7, graph);
insertEdge(5, 6, graph);
insertEdge(6, 4, graph);
PrintGraph(graph);
int * res=Topology_sort(graph, queue);
printf("\n위상정렬알고리즘 수행 결과:\n");
for (int i = 0; i < 7; i++) {
printf("%d ", res[i]);
}
getchar();
return 0;
}
ver2)방문배열을 설정하여 dequeue할때마다 해당 노드의 visited를 true로 변환하면서 while문을 다 돌고 난 후, visited배열에 방문하지 않는 노드가 존재한다면 위상 정렬 실패이고 아닌 경우엔 정렬된 결과를 출력
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>
#define MAX_SIZE 100
typedef struct _NODE_ {
int vertex;
struct _NODE_* link;
}NODE;
typedef struct _GRAPH_ {
NODE** head;
int n; //정점의 갯수
}GRAPH;
typedef struct _Q_NODE_ {
int data;
struct _Q_NODE_ *link;
}Q_NODE;
typedef struct _Q_TYPE_ {
Q_NODE* front;
Q_NODE* rear;
}Q_TYPE;
void init(Q_TYPE * queue) {
queue->front = NULL;
queue->rear = NULL;
}
int IsEmpty(Q_TYPE* queue) {
return queue->front == NULL;
}
void EnQueue(Q_TYPE* queue, int item) {
Q_NODE* newNode = (Q_NODE*)calloc(1, sizeof(Q_NODE));
assert(newNode != NULL);
newNode->data = item;
newNode->link = NULL;
if (IsEmpty(queue)) {
queue->front = newNode;
queue->rear = newNode;
}
else {
Q_NODE* curNode = queue->rear;
curNode->link = newNode;
queue->rear = newNode;
}
}
int DeQueue(Q_TYPE* queue) {
if (IsEmpty(queue)) {
printf("꺼낼 큐노드가 존재하지 않습니다\n");
return;
}
else {
int qdata = queue->front->data;
Q_NODE* curNode = queue->front;
queue->front = queue->front->link;
free(curNode);
curNode = NULL;
return qdata;
}
}
void Top_Sort(GRAPH *g, Q_TYPE* queue, int * degree, int n) {
int* res = (int*)calloc(n, sizeof(int));
int i = 0;
bool* visited = (bool*)calloc(n, sizeof(bool));
assert(visited != NULL);
assert(res != NULL);
//초기설정: 진입차수가 0인 노드 큐에 삽입
for (int i = 0; i < n; i++) {
if (degree[i] == 0) {
EnQueue(queue, i);
}
}
while (!IsEmpty(queue)) {
int now = DeQueue(queue);
res[i++] = now;
visited[now] = true;
NODE* curNode = g->head[now];
while (curNode != NULL) {
degree[curNode->vertex] -= 1;
if (degree[curNode->vertex] == 0 && visited[curNode->vertex] != true) {
EnQueue(queue, curNode->vertex);
}
curNode = curNode->link;
}
}
for (int i = 0; i < n; i++) {
if (visited[i] == false) {
printf("위상 정렬 수행 실패\n");
return;
}
}
printf("위상 정렬 수행결과 \n");
for (int i = 0; i < n; i++) {
printf("%d ", res[i]+1);
}
}
GRAPH* MakeGraph(int n) {
GRAPH* g = (GRAPH*)calloc(1, sizeof(GRAPH));
assert(g != NULL);
g->head = (NODE**)calloc(n, sizeof(NODE*));
assert(g->head != NULL);
return g;
}
void insertVertex(int vertex, GRAPH* g) {
if (g->n > MAX_SIZE) {
printf("더이상 정점을 삽입할 수 없습니다\n");
return;
}
else {
g->n++;
}
}
void insertEdge(int u, int v, GRAPH* g) {
if (u >= g->n || v >= g->n) {
printf("해당 정점은 그래프에 존재하지 않습니다\n");
return;
}
else {
NODE* newNode = NULL;
newNode = (NODE*)calloc(1, sizeof(NODE));
assert(newNode != NULL);
newNode->vertex = v;
newNode->link = NULL;
NODE* curNode = g->head[u];
NODE* preNode = curNode;
if (g->head[u] == NULL) {
g->head[u] = newNode;
return;
}
else if (g->head[u] != NULL) {
if (g->head[u]->vertex > newNode->vertex) {
newNode->link = g->head[u];
g->head[u] = newNode;
return;
}
}
curNode = curNode->link;
while (curNode != NULL) {
preNode = curNode;
if (curNode->vertex > newNode->vertex) {
break;
}
curNode = curNode->link;
}
newNode->link = preNode->link;
preNode->link = newNode;
}
}
void PrintGraph(GRAPH* g) {
for (int i = 0; i < g->n; i++) {
printf("[Header Node: %d] ", i);
NODE* curNode = g->head[i];
while (curNode != NULL) {
printf("-> %d ", curNode->vertex);
curNode = curNode->link;
}
printf("\n");
}
}
int * Degree(GRAPH* g) {
int* degree = (int*)calloc(g->n, sizeof(int));
assert(degree != NULL);
for (int i = 0; i < g->n; i++) {
NODE* curNode = g->head[i];
while (curNode != NULL) {
degree[curNode->vertex] += 1;
curNode = curNode->link;
}
}
return degree;
}
void PrintDegree(GRAPH *g,int* degree) {
for (int i = 0; i < g->n; i++) {
printf("%d ", degree[i]);
}
}
int main() {
GRAPH* graph = MakeGraph(7);
for (int i = 0; i < 7; i++) {
insertVertex(i, graph);
}
insertEdge(0, 1, graph);
insertEdge(0, 4, graph);
insertEdge(1, 2, graph);
insertEdge(2, 3, graph);
insertEdge(3, 5, graph);
insertEdge(4, 5, graph);
insertEdge(5, 6, graph);
PrintGraph(graph);
int* degree = Degree(graph);
Q_TYPE* queue = (Q_TYPE*)calloc(1, sizeof(Q_TYPE));
assert(queue != NULL);
init(queue);
Top_Sort(graph, queue, degree, 7);
getchar();
return 0;
}
'C > 알고리즘' 카테고리의 다른 글
| 스택 응용(수식 계산) (0) | 2023.09.15 |
|---|---|
| 강한 결합 요소(Strongly Connected Components) (0) | 2023.08.15 |
| Floyd Washall Algorithm(플로이드 와샬 알고리즘) (0) | 2023.08.14 |
| Dijkstra Algorithm[C] (0) | 2023.08.11 |
| kruskal algorithm[c] (0) | 2023.07.31 |



