1. 다익스트라 알고리즘
1-1. 순차탐색을 이용한 다익스트라
INF = int(1e9)
def get_min_distance(res, visited):
min_val = INF
idx=0
for i in range(1,len(res)):
if(visited[i]==0 and min_val>res[i]):
min_val = res[i]
idx = i
return idx
def dijkstra(graph, E,V, start, res):
visited = [0]*(V+1)
#초기화
res[start]=0
for j in range(1,V+1):
for i in range(1,V+1):
now= get_min_distance(res,visited)
visited[now]=1
for now_to, distance in graph[now]:
if(res[now]+distance < res[now_to]):
res[now_to]=res[now]+distance
#print(f"STEP {j}: distance: {res[1:]}")
#print(f" found: {visited[1:]}")
#print()
print(res[1:])
def main():
print("간선의 갯수와 정점의 갯수를 정하시오 ")
E,V = map(int,input().split())
graph=[[] for _ in range(V+1)]
print("출발 정점, 도착 정점, 거리 정하시오")
for _ in range(E):
#[[2,3]] : 1번째 정점->2번째 정점 (거리:3)
start, to, distance = map(int, input().split())
graph[start].append([to,distance])
for i in range(1,V+1):
res=[INF]*(V+1)
print("start : {}".format(i))
dijkstra(graph, E,V, i,res)
print("----------------------------------")
if __name__=="__main__":
main()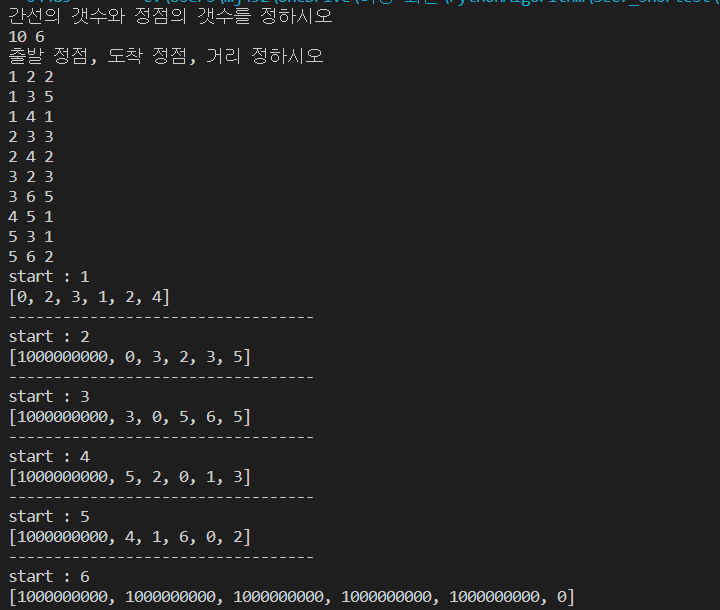
1-2. 우선순위 큐를 이용한 다익스트라
import heapq
INF = int(1e9)
def dijkstra(graph, V, distance,start):
distance[start]=0
heap =[]
#(거리, 노드)순으로 힙에 삽입한다
heapq.heappush(heap,(0,start))
while(heap):
val,now = heapq.heappop(heap)
if(val > distance[now]):
continue
for now_to, dis in graph[now]:
if(val+dis<distance[now_to]):
distance[now_to]=val+dis
heapq.heappush(heap, (distance[now_to], now_to))
def main():
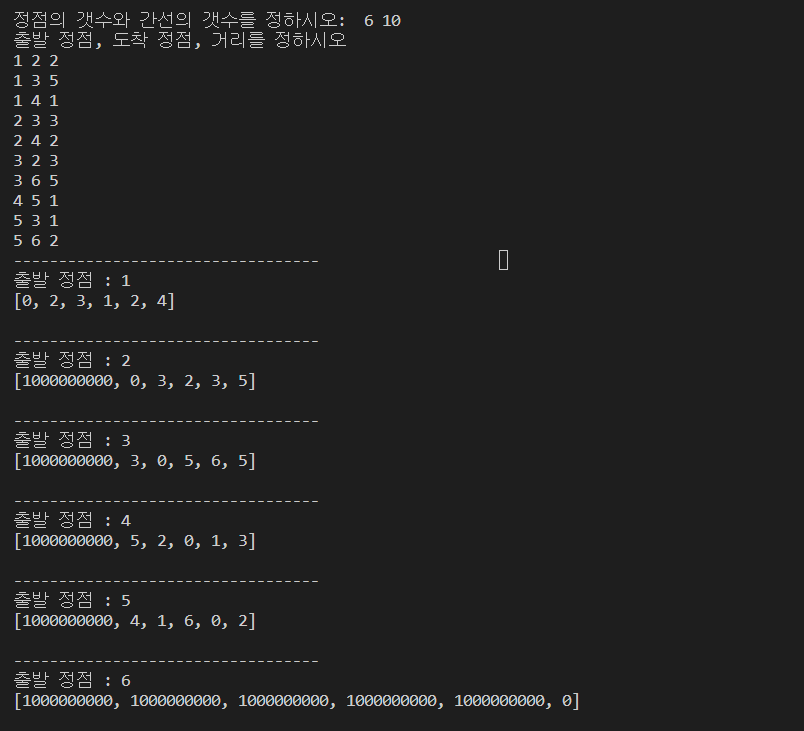
print("정점의 갯수와 간선의 갯수를 정하시오: ", end=" ")
V,E = map(int, input().split())
graph=[[] for _ in range(V+1)]
print("출발 정점, 도착 정점, 거리를 정하시오 ")
for _ in range(E):
start, end, val= map(int, input().split())
graph[start].append((end,val))
for i in range(1,V+1):
print("----------------------------------")
print(f"출발 정점 : {i}")
distance=[INF]*(V+1)
dijkstra(graph,V,distance,i)
print(distance[1:])
print()
if __name__=="__main__":
main()
cf> 참고
이때, 아래 코드에서 크거나 같으면 안되는 이유는 처음에 세팅할 때 출발정점에 대해서는 distance값을 0으로 설정하는데 heapq에 push할 때 (0, start) 튜플을 삽입하기에 해당 조건문을 통과시키기 위해 ≥는 불가능하다
if(val > distance[now]): continue
2. 플로이드 와샬 알고리즘
INF = int(1e9)
def Floyd_Washall(graph,V):
res=[[0]*(V) for _ in range(V)]
for i in range(V):
for j in range(V):
if(graph[i][j]==-1):
res[i][j]=INF
else:
res[i][j]=graph[i][j]
for mid in range(V):
for start in range(V):
for end in range(V):
if(mid==start or mid==end or start==end):
continue
else:
if(res[start][mid]+res[mid][end]<res[start][end]):
res[start][end]=res[start][mid]+res[mid][end]
for i in range(V):
for j in range(V):
print(res[i][j], end=" ")
print()
def main():
V= int(input("정점의 갯수를 정하시오"))
graph = []
for i in range(V):
graph.append(list(map(int,input().split())))
print(graph)
Floyd_Washall(graph,V)
if __name__=="__main__":
main()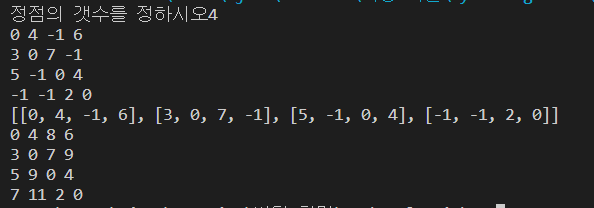
3. 예제
(1) 전보
import heapq
INF= int(1e9)
def dijkstra(graph, N, start,distance):
heap = []
heapq.heappush(heap,(0, start))
distance[start]=0
while(heap):
#start->now까지 걸리는 시간
value, now = heapq.heappop(heap)
#이때 start->now까지 걸리는 시간이 업뎃해주는 표의 시간보다 더 걸린다면 pass
if(value >distance[now]):
continue
for now_to, time in graph[now]:
if(value+time < distance[now_to]):
distance[now_to]=value+time
heapq.heappush(heap,(distance[now_to],now_to))
total=0 #총 걸리는 시간
num=0 #메세지 받는 도시
for i in range(1,N+1):
if(distance[i]!=INF and i!=start):
total +=distance[i]
num+=1
return total, num
def main():
#도시의 갯수, 통로의 갯수, 메세지 보내고자 하는 도시
N,M,C = map(int, input().split())
graph=[[] for _ in range(N+1)]
for i in range(M):
#출발점, 도착점, 걸리는 시간
X,Y,Z = map(int, input().split())
graph[X].append((Y,Z))
distance=[INF]*(N+1)
#메세지를 받는 도시의 갯수와 걸리는 시간 출력(이때 자기자신은 제외)
total, num = dijkstra(graph, N,C, distance)
print(num, total)
if __name__=="__main__":
main()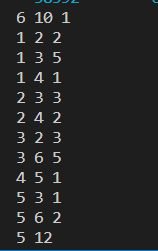
(2)미래 도시
1) 우선순위 큐 이용한 다익스트라로 구현
import heapq
INF = int(1e9)
def dijkstra(graph, N,start, end):
res=[INF]*(N+1)
res[start]=0
heap=[]
heapq.heappush(heap, (0,start))
while(heap):
time, now = heapq.heappop(heap)
if(time > res[now]):
continue
for time_to, now_to in graph[now]:
if(time+time_to < res[now_to]):
res[now_to]=time+time_to
heapq.heappush(heap,(res[now_to], now_to))
return res[end]
def main():
#전체 회사의 개수, 경로의 개수
N,M = map(int, input().split())
graph=[[] for _ in range(N+1)]
for _ in range(M):
start, end = map(int, input().split())
graph[start].append((1,end))
graph[end].append((1,start))
#물건 판매하러 가는 최종 목적지, 중간에 커피 마시는 곳
X,K= map(int, input().split())
start_K=dijkstra(graph,N,1,K)
K_X = dijkstra(graph,N,K,X)
if(start_K ==INF or K_X ==INF):
print(-1)
else:
print(start_K+K_X)
if __name__=="__main__":
main()
2) 플로이드 와샬 알고리즘 이용
INF = int(1e9)
def Floyd_Washall(graph,N, start, end):
distance=[[0]*N for _ in range(N)]
for i in range(N):
for j in range(N):
distance[i][j]=graph[i][j]
for mid in range(N):
for s in range(N):
for e in range(N):
if(mid!=s and mid!=e and s!=e):
if(distance[s][mid]+distance[mid][e]<distance[s][e]):
distance[s][e]=distance[s][mid]+distance[mid][e]
return distance[start][end]
def main():
#전체 회사갯수, 경로 갯수
N,M = map(int, input().split())
graph =[[INF]*(N) for _ in range(N)]
for i in range(N):
for j in range(N):
if(i==j):
graph[i][j]=0
for _ in range(M):
start, end = map(int, input().split())
graph[start-1][end-1]=1
graph[end-1][start-1]=1
#최종목적지, 거쳐가는 곳
X, K = map(int, input().split())
start_K=Floyd_Washall(graph,N, 0, K-1)
K_X = Floyd_Washall(graph, N,K-1,X-1)
if(start_K == INF or K_X==INF):
print(-1)
else:
print(start_K + K_X)
if __name__=="__main__":
main()
'Python > 알고리즘' 카테고리의 다른 글
| [Python]바이너리 인덱스 트리(Binary Indexed Tree) (2) | 2023.10.10 |
|---|---|
| [Python]기타 알고리즘 (0) | 2023.10.06 |
| 이진탐색(Binary Search) (0) | 2023.09.19 |
| DFS&BFS 문제 (0) | 2023.09.04 |
| DFS&BFS[python] (0) | 2023.09.04 |



