1. 최소 공통 조상
: 두 노드의 가장 가까운 공통 조상 노드를 구하는 것
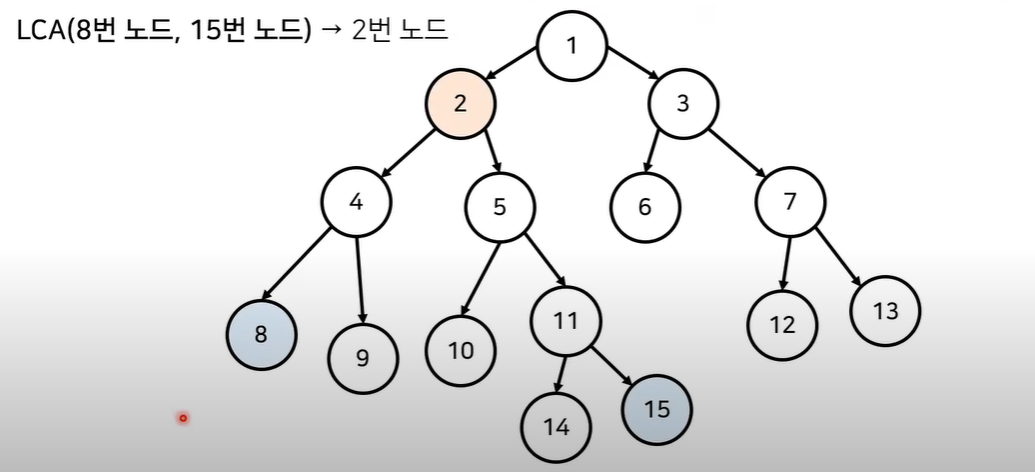
1-1. 단순 LCA 알고리즘
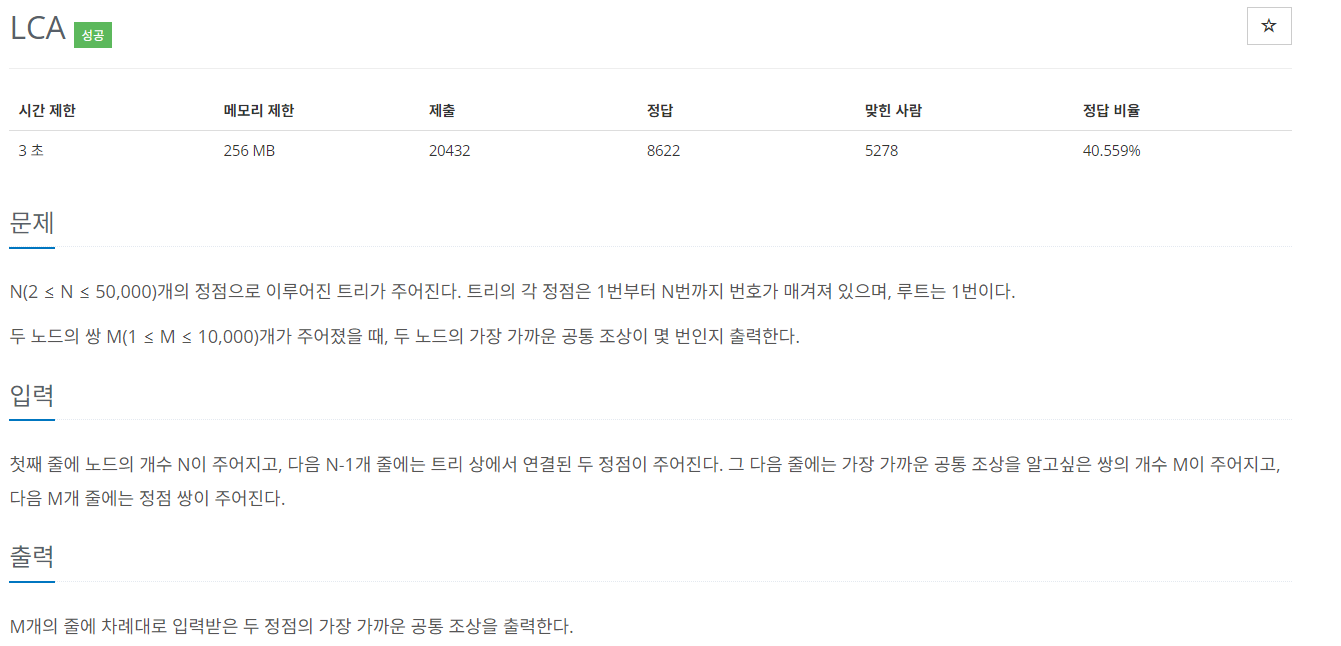
1-1-1. 알고리즘 동작 과정
- 모든 노드에 대한 깊이 계산
- 최소 공통 조상을 찾을 두 노드 확인
- 두 노드의 깊이가 동일하도록 함
- 두 노드의 부모가 같아질때까지 반복적으로 두 노드의 부모 방향으로 거슬러 올라감
(1) 깊이 계산
: BFS(너비 우선 탐색 이용)
=> 깊이 계산 동작 과정 아래 그림처럼 단순예제로 표현

from collections import deque
def BFS(start):
queue = deque()
queue.append(start)
visited[start]=True
while(queue):
now = queue.popleft()
for node in graph[now]:
if(visited[node]!=True):
visited[node]=True
parent[node]=now
depth[node]=depth[now]+1
queue.append(node)
(2) 깊이 맞추기
while(depth[a]!=depth[b]):
if(depth[a]<depth[b]):
b = parent[b]
else:
a=parent[a]
(3) 깊이 맞추고 나면 같이 거슬러올라가며 조상 노드 찾기
while(a!=b):
a= parent[a]
b= parent[b]
return a1-1-2. 구현 (전체 소스코드)
import sys
from collections import deque
input = sys.stdin.readline
N= int(input().rstrip()) #정점의 갯수
visited=[False]*(N+1)
parent=[0]*(N+1)
depth=[0]*(N+1)
graph=[[] for _ in range(N+1)]
for _ in range(N-1):
a,b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
def BFS(start):
queue = deque()
queue.append(start)
visited[start]=True
while(queue):
now = queue.popleft()
for node in graph[now]:
if(visited[node]!=True):
visited[node]=True
parent[node]=now
depth[node]=depth[now]+1
queue.append(node)
def LCA(a,b):
while(depth[a]!=depth[b]):
if(depth[a]<depth[b]):
b= parent[b]
else:
a= parent[a]
if a==b:
return a
while(a!=b):
a = parent[a]
b= parent[b]
return a
res=[]
M = int(input().rstrip())
BFS(1)
for _ in range(M):
a,b = map(int, input().split())
res.append(LCA(a,b))
for i in res:
print(i)1-1-3. 알고리즘 복잡도
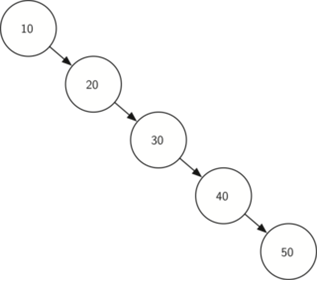
: 부모 방향으로 거슬러 올라가기 위해 아래와 같이 편향트리같은 최악의 경우 O(N)의 시간 복잡도 요구
: 모든 쿼리(M)을 처리할 때의 시간 복잡도는 O(NM)
1-2. LCA 알고리즘 개선
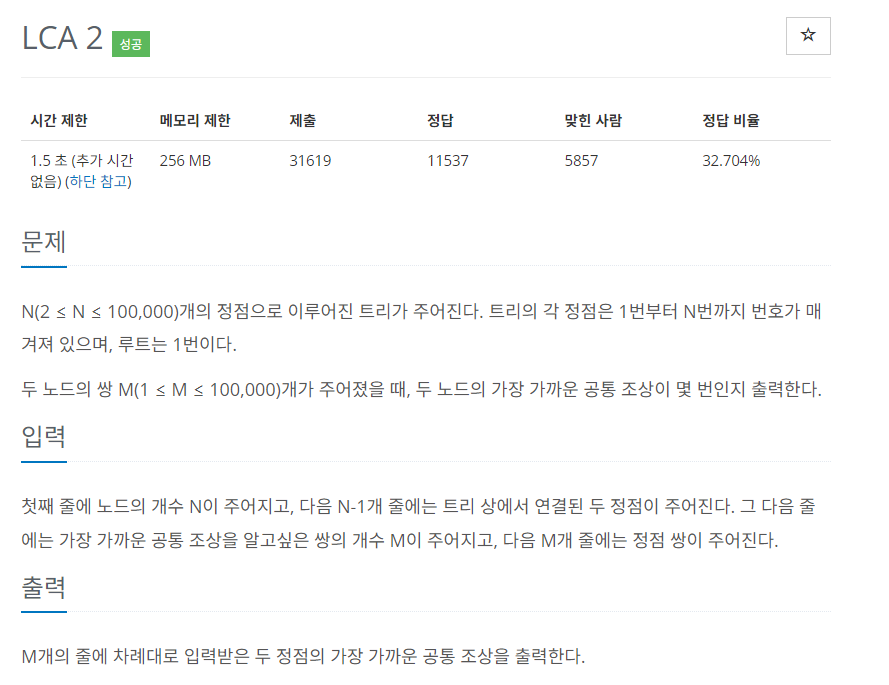
1-2-1. 알고리즘 동작 과정
- BFS 통해 모든 노드의 2^0번째 부모 노드 구함
- 이중 반복문 통해 모든 노드의 2^17번째 부모 노드까지 구함
- LCA 찾고자하는 두 노드의 깊이 맞춤
- 깊이 맞추고 나면 올라가며 LCA 찾음
(1) 부모
: 노드를 올라갈 때 1칸씩 올라갔다면 1->2->4->8칸씩 2^i만큼 2의 제곱 형태로 올라간다
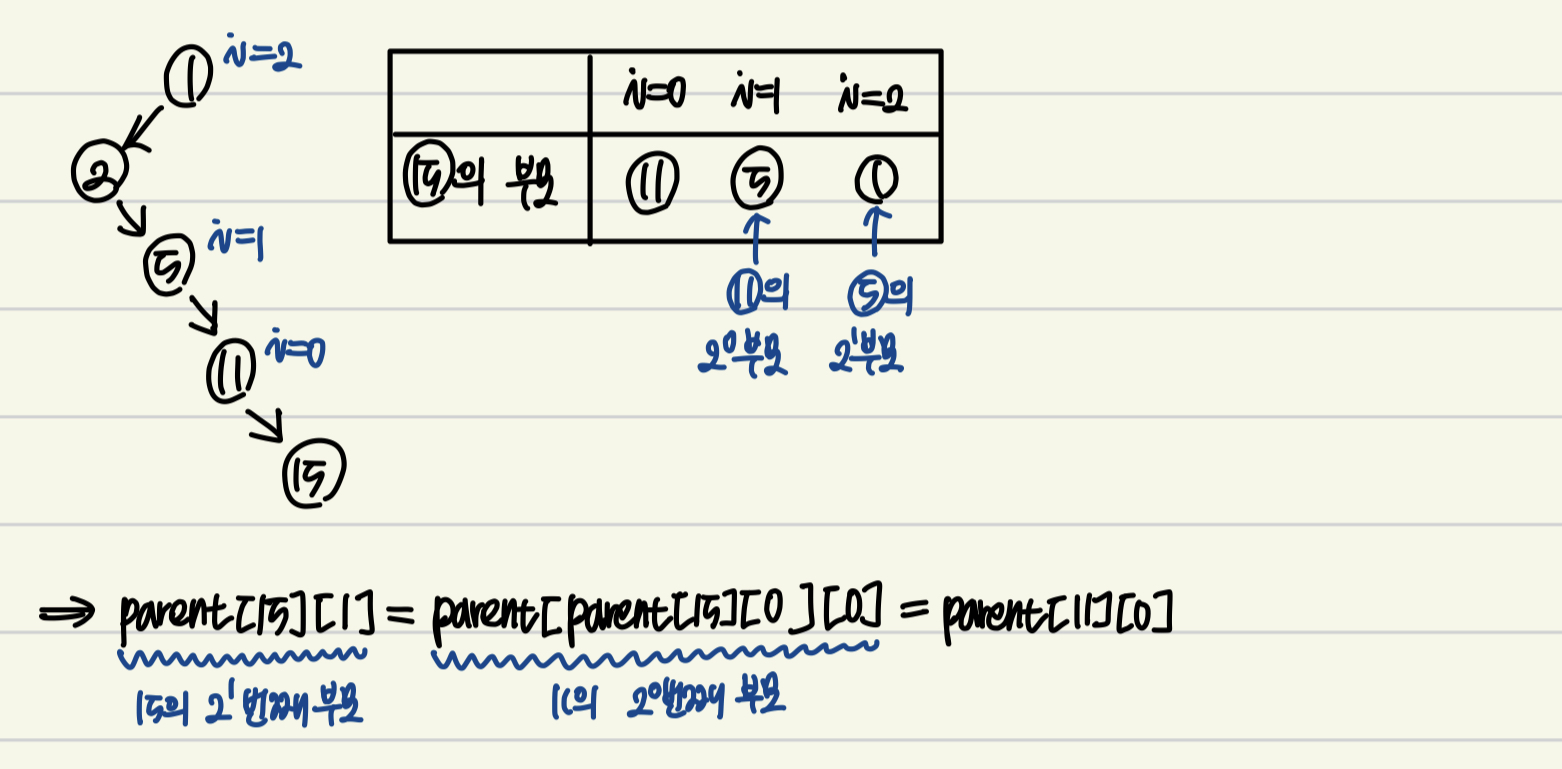
ex) i=1 : 노드의 2^1번째 부모
=> 이때 노드 15의 2^1번째 부모 = 노드 15의 2^0번째 부모의 2^0번째 부모
=> 일반화 : parent[node][i] = parent[parent[node][i-1]][i-1]
(2) 몇번째 부모까지 구할 수 있을까

=> 해당 문제에서 노드의 최대 갯수는 100,000이기에 편향트리라고 가정했을때 최대 구할 수 있는 부모는 2^17번째 부모임을 알 수 있다
=> 이때 노드의 2^0,2^1,...2^17번째 부모까지 구할 수 있으므로 최대 18번 올라갈 수 있음을 알 수 있다
(3) 전체 부모 설정
: 행과 열 설정 주의하자!
#잘못된 코드
for i in range(1,NODE+1):
for j in range(1, INF):
parent[i][j]= parent[parent[i][j-1]][j-1]
#올바른 코드
for pos in range(1,INF):
for node in range(1,N+1):
parent[node][pos]= parent[parent[node][pos-1]][pos-1]=> 전체 부모를 구하기 전에 bfs 탐색 통해 모든 노드의 2^0번째 부모도 같이 저장해놓는다
=> 따라서, bfs 탐색하고 나면 모든 노드는 2^0번째 부모노드만 저장하고있기때문에 잘못된 코드로 작성한다면
왼쪽 사진과 같이 노드 15의 2^2번째 부모 노드를 구하고자 할 때 에러가 발생한다
=> 위에서부터 부모 노드들을 갱신해나가야한다


(4) LCA 찾기
: 두 노드의 LCA를 찾기 위해서는 크게 2가지의 과정이 필요하다
- 두 노드의 깊이 맞추기
- 깊이 맞추고 나면 위로 올라가며 LCA 찾기
=> 여기서 핵심은 LCA 알고리즘은 (a의 k번째 조상) = (b의 k번째 조상)인 최소 k를 찾는 것이 아닌
(a의 k번째 조상) ≠ (b의 k번째 조상)인 최대 k를 찾아 a(or b)의 2^0번째 부모 노드(=LCA)를 찾는 것이다!

1) 깊이 맞추기
: 두 노드의 깊이 차를 이용하였다
: 여기서 핵심은 깊이 차를 구하고 그 값의 이진수를 이용하는 것이다
ex) 11(10) -> 1011(2)인데 bit값이 0인 경우엔 jump하지않고 bit값이 1인 경우에 jump하는 것이다
=> 1011 ( 2^3 + 2^2 + 2^1 + 2^0 )
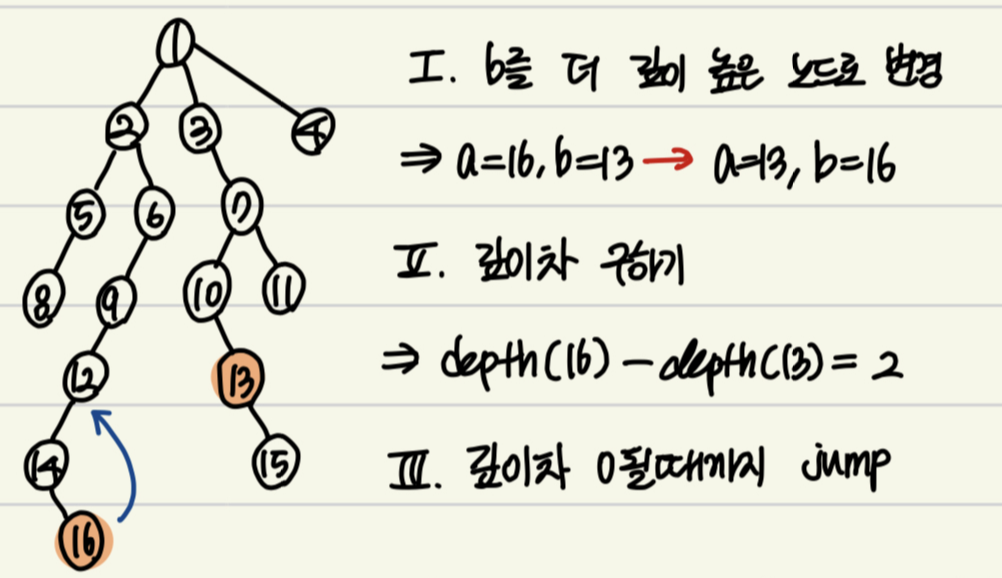

=> 반복문을 통해 LSB부터 차근차근 1bit씩 1인지 아닌지 diff%2 연산을 통해 확인하고 1이면 이진수로 나타났을 때 그 bit가 1이라는 것이기에 해당 노드를 그 값만큼 jump한다
cf> 이때 깊이를 맞추고 나서 두 노드의 깊이가 같다면 바로 그 두 노드의 부모노드가 LCA인 경우이므로 LCA찾기 과정은 수행하지 않고 바로 parent[a][0] 또는 parent[b][0] 값을 return한다

#깊이 맞추기 수행 후
if(a==b):
return a
2) LCA 찾기
: 깊이를 맞추고 났다면 이제 본격적으로 LCA를 찾아야한다
: 처음에 이 LCA 알고리즘을 공부할 때 노드들을 거슬러 올라가게 한다면서 왜 반복문은 최댓값(노드:N일때, log2(N))부터 시작하는거지라며 이해를 하지 못했었는데 "두 노드를 두 노드의 첫번째 부모부터 차근차근 올라가게한다" 가 아닌 "최대한 멀리서부터 출발하여(반복문 최댓값인 이유) 두 노드를 위로 거슬러올라가게한다" 였다
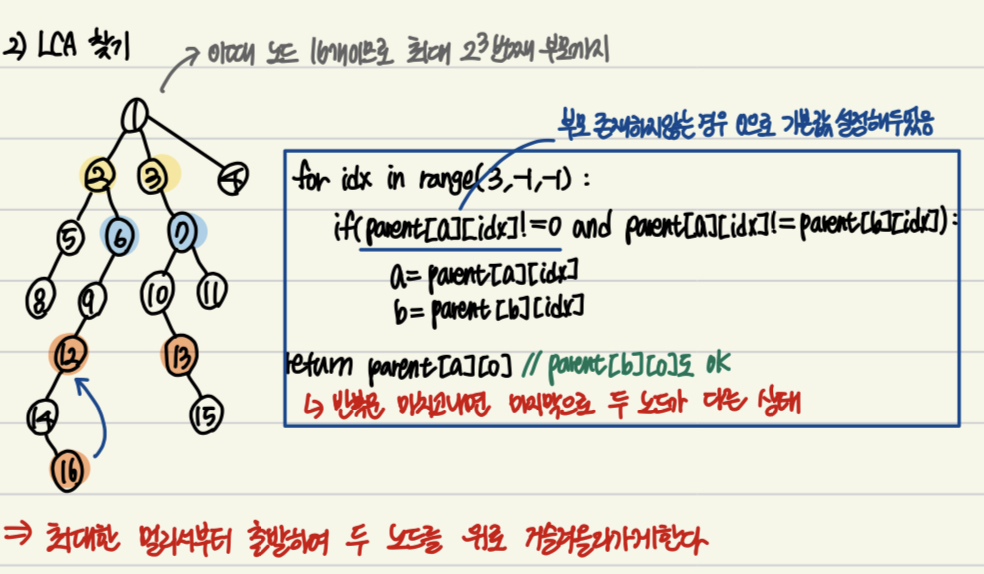

for idx in range(INF-1, -1,-1):
if(parent[a][idx]!=parent[b][idx]):
a= parent[a][idx]
b= parent[b][idx]
return parent[a][0]
cf> 남들한텐 당연히 이렇지일 수 있지만 나는 아래의 두가지를 이해를 못했다
① 왜 반복문을 다 수행하고 나면 마지막으로 두 노드의 값이 다른거지?
(+ 바보같을 수 있지만 0까지 돌려야하는 건 알겠는데 왜 0까지 돌려야하지?라며 깊게 생각했었다)
② 반복문을 수행하다가 두 노드의 값이 다르면 해당 노드로 update 시키는 것까진 알겠는데 왜 그럼 반복문 idx값을 처음부터 안돌려도 되는거지?

②부터 말하자면, 이해하기 쉽게 처음으로 두 노드 값이 다른 경우를 찾았을 때라고 가정하자
: k번째부터 내려오다가 k-1번째서 노드 값이 다름(= 두 노드의 2^k번째 부모부터 구하면서 내려오다가 두 노드의 2^(k-1)번째 부모 값이 다름)
=> 노드 a,b 의 LCA를 찾고자하는 경우 ( 이때 마지막으로 같은 두 노드의 부모 노드 : c , 처음으로 다른 값이 나온 a와 b의 부모 노드 : a', b')
=> c는 a와 b의 2^k번째 부모임과 동시에 a'와 b'의 2^(k-1)번째 부모이다
=> a'와 b'의 2^k번째부모부터는 당연히 다 같은 노드일테니 새롭게 반복문 idx값을 처음부터 안돌려도 되는 것이다
- a의 2^k번째 부모 노드 = c == b의 2^k번째 부모 노드 (idx = k)
=> 값이 같으므로 아무것도 하지않음 - a의 2^(k-1)번째 부모 노드 = a' != b의 2^(k-1)번째 부모 노드 (idx = k-1)
=> 값이 다르므로 a->a', b->b' 노드 update - a'의 2^(k-2)번째 부모 노드와 b'의 2^(k-2)번째 부모 노드 값을 구하며 계속 반복문 수행하며 노드 update (idx = k-2)
=> 이때 a'와 b'의 2^(k-1)번째 부모노드는 c이기에 idx값을 처음부터 k로 설정하지않아도됨(내가 궁금했던 것)
=> 참고로, 만약 c가 2^8과 같이 큰 값이었다면 a', b'와 거리가 꽤 많이 차이나기에 그 사이에 아직 같은 노드인 경우가 있을 수도 있다
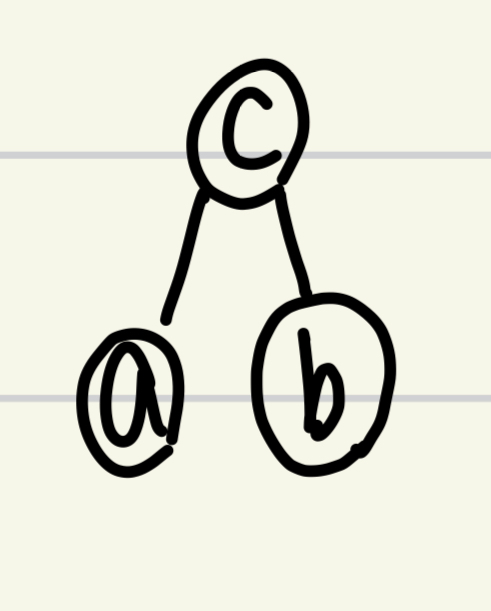
①은 ②를 이해한다면 저절로 이해할 수 있다. 반복문을 수행하다보면 두 노드는 계속 올라갈 것이고 그 두 노드는 필연적으로 마지막으로 두 노드가 다른 상태이다. 그렇기에 두 노드 중 아무 노드의 2^0번째 부모노드 (= 바로 위)가 LCA가 된다
=> 이때 아래와 같은 경우는 처음 두 노드를 계속해서 update하지 않게되는데 어차피 반복문 통해 바로 위 부모노드까지 탐색하기에(idx=0) 문제되지 않는다 (나는 update 계속되지않는 경우도 궁금했었다)
1-2-2. 전체 소스코드
import sys
from collections import deque
input = sys.stdin.readline
N = int(input().rstrip()) #노드의 갯수
graph=[[]for _ in range(N+1)]
INF = 18 #최대 18번 올라갈 수 있음
#2^17번째 부모노드까지 구할 수 있음
parent=[[0]*INF for _ in range(N+1)]
visited=[False]*(N+1)
depth=[0]*(N+1)
for _ in range(N-1):
a,b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
def set_first_parent(start):
queue = deque()
queue.append(start)
visited[start]=True
while(queue):
now= queue.popleft()
for node in graph[now]:
if(visited[node]!=True):
visited[node]=True
parent[node][0]= now
depth[node]= depth[now]+1
queue.append(node)
def set_all_parent():
set_first_parent(1)
for pos in range(1,INF):
for node in range(1,N+1):
parent[node][pos]= parent[parent[node][pos-1]][pos-1]
def LCA(a,b):
if(depth[b]<depth[a]):
a,b=b,a
diff = depth[b]-depth[a]
i=0
while(diff!=0):
if(diff%2==1):
b= parent[b][i]
diff//=2
i+=1
if(a==b):
return a
for idx in range(INF-1, -1,-1):
if(parent[a][idx]!=parent[b][idx]):
a= parent[a][idx]
b= parent[b][idx]
return parent[a][0]
M = int(input().rstrip())
res=[]
set_all_parent()
for _ in range(M):
a,b = map(int, input().split())
res.append(LCA(a,b))
for i in res:
print(i)1-2-3. 알고리즘 복잡도
: 부모 방향으로 거슬러 올라가기 위해 O(logN)
: 모든 쿼리(M)을 처리할 때의 시간 복잡도는 O(MlogN)
'Python > 알고리즘' 카테고리의 다른 글
| [python] 스택 응용 : 미로 문제 (0) | 2023.11.20 |
|---|---|
| [Python] 스택 응용 : 후위 표기법 이용한 수식 계산 (0) | 2023.11.15 |
| [Python]바이너리 인덱스 트리(Binary Indexed Tree) (2) | 2023.10.10 |
| [Python]기타 알고리즘 (0) | 2023.10.06 |
| [Python]최단 경로 알고리즘 : Dijkstra Algorithm, Floyd Washall (0) | 2023.09.26 |



