1. 이진 트리
1-1. 이진 트리 기본 동작 구현
- inorder() : LVR
- preorder() : VLR
- postorder() : LRV
- getSize() : 모든 노드의 개수 세는 함수
- getHeight() : 트리의 높이 반환하는 함수
- containBT() : 트리에 특정 키를 갖는 노드 있는지 true/false로 반환하는 함수
1-1-1. 코드 구현
: 아래와 같은 트리로 구성되게 함
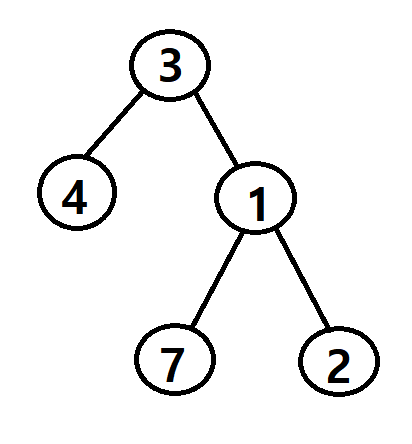
Binary_tree.h
#pragma once #include <iostream> using namespace std; class TreeNode { private: int key; TreeNode* left; TreeNode* right; public: TreeNode(int item) :key(item), left(NULL), right(NULL) {}; TreeNode(int item, TreeNode* l, TreeNode* r) : key(item), left(l), right(r) {}; int getKey() { return key; } void setLeft(TreeNode* item) { left = item; } void setRight(TreeNode* item) { right = item; } friend class Tree; }; class Tree { private: TreeNode* root; public: Tree() : root(NULL) {} TreeNode* getRoot() { return root; } void setRoot(TreeNode* item) { root = item; } void inorder(TreeNode* root) { if (root == NULL) { return; } inorder(root->left); cout << root->key << " "; inorder(root->right); } void preorder(TreeNode* root) { if (root == NULL) { return; } cout << root->key; preorder(root->left); preorder(root->right); } void postorder(TreeNode* root) { if (root == NULL) { return; } postorder(root->left); postorder(root->right); cout << root->key; } int getSize(TreeNode* root) { if (root == NULL) { return 0; } return getSize(root->left) + getSize(root->right) + 1; } int getHeight(TreeNode* root) { if (root == NULL) { return 0; } return max(getHeight(root->left), getHeight(root->right)) + 1; } bool containsBT(TreeNode* root, int key) { if (root == NULL) { return false; } if (key == root->key) { return true; } return containsBT(root->left, key) || containsBT(root->right, key); } };
main.cpp
#include "Binary_tree.h" #include <iostream> using namespace std; int main() { TreeNode* left = new TreeNode(4); TreeNode* right = new TreeNode(1); Tree* tr = new Tree(); TreeNode* item = new TreeNode(3, left, right); tr->setRoot(item); right->setLeft(new TreeNode(7)); right->setRight(new TreeNode(2)); cout << "\n[이진트리 출력]\n"; tr->inorder(tr->getRoot()); cout << "\n[이진트리 높이]\n"; cout << tr->getHeight(tr->getRoot()); cout << "\n[이진트리 노드의 개수]\n"; cout << tr->getSize(tr->getRoot()); cout << "\n[이진트리에 노드 2가 존재하는지 확인]\n"; if (tr->containsBT(tr->getRoot(), 2) == true) { cout << "Exist\n"; } else { cout << "No Exist\n"; } return 0; }

1-2. 이진트리 특수 함수
(1) 트리에서 가장 큰 key를 가지는 노드 찾아서 반환하는 함수
- maximumBT() : 최대 key가지는 노드 반환하는 함수
- Max() : 두 노드 중 더 큰 key가지는 노드 반환하는 함수
TreeNode* Max(TreeNode* left, TreeNode* right) {
if (left == NULL && right != NULL) {
return right;
}
else if (left != NULL && right == NULL) {
return left;
}
else if (left == NULL && right == NULL) {
return NULL;
}
else {
return left->key<right->key?right:left;
}
}
TreeNode* maximumBT(TreeNode* root) {
if (root == NULL) {
return NULL;
}
TreeNode* maxNode = root;
TreeNode* cmp = Max(maximumBT(root->left), maximumBT(root->right));
if (cmp != NULL && maxNode->key < cmp->key) {
maxNode = cmp;
}
return maxNode;
}

(2) 레벨 순회하는 함수
- levelorder() : level order traversal 동작 함수
→ STL <queue> 이용
void levelorder() {
queue <TreeNode*> que;
que.push(root);
while (que.size()) {
TreeNode * now = que.front();
que.pop();
cout << now->key << " ";
if (now->left != NULL) {
que.push(now->left);
}
if (now->right != NULL) {
que.push(now->right);
}
}
}
(3) 특정 노드까지 도달한 경로 출력
- findPath() : 모든 노드 순회하며 특정 key갖는 노드 찾는 함수
- printStack() : 스택 출력하는 함수
1) 알고리즘 동작 순서
- 해당 노드가 존재하지 않으면 false 반환
→ 그렇지않다면, 해당 노드 stack에 push
+
해당 노드의 키값이 찾고자 하는 키값과 같다면 true반환
→ 그렇지않다면, 왼쪽자식노드와 오른쪽자식노드를 각각 재귀문을 돌림
→ 이때, 둘 중 하나가 true를 반환하면 true 반환
→ 모두 false를 반환하면 stack에서 pop하고 false 반환
2) 동작 과정

main.cpp
#include "Binary_tree.h" #include <iostream> #include <vector> using namespace std; void printStack(vector <TreeNode*>& stack) { for (int i = 0; i < stack.size(); i++) { TreeNode* curNode = stack[i]; cout << curNode->getKey(); if (i != stack.size() - 1) { cout << " -> "; } } }
Binary_tree.h
bool findPath(TreeNode* root, int key, vector <TreeNode*>& stack) { if (root == NULL) { return false; } stack.push_back(root); if (root->key == key) { return true; } if (findPath(root->left, key, stack) || findPath(root->right, key, stack)) { return true; } else { stack.pop_back(); return false; } }

(4) LCA ( 최소 공통 조상 찾기 )
≪cf≫최소공통조상 개념
2023.10.12 - [Python/알고리즘] - 최소 공통 조상(Lowest Common Ancestor)
최소 공통 조상(Lowest Common Ancestor)
1. 최소 공통 조상 : 두 노드의 가장 가까운 공통 조상 노드를 구하는 것 1-1. 단순 LCA 알고리즘 1-1-1. 알고리즘 동작 과정 모든 노드에 대한 깊이 계산 최소 공통 조상을 찾을 두 노드 확인 - 두 노
growingupis.tistory.com
TreeNode* LCA(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == NULL) {
return NULL;
}
if (root == p || root == q) {
return root;
}
TreeNode* left = LCA(root->left, p, q);
TreeNode* right = LCA(root->right, p, q);
if (left != NULL && right!=NULL) {
return root;
}
else if (left != NULL) {
return left;
}
else if (right != NULL) {
return right;
}
else {
return NULL;
}
}
'C++ > 알고리즘' 카테고리의 다른 글
| [C++] 이분 그래프(Bigraph) (0) | 2023.12.13 |
|---|---|
| [C++] BST Operations (1) | 2023.12.07 |
| [C++]Shuffle Doubly linked list (0) | 2023.11.30 |
| [C++]Split Doubly Linked List (0) | 2023.11.29 |
| [c++] 연결리스트 이용한 다항식 덧셈/뺄셈/곱셈 (0) | 2023.11.28 |



