1. Heap(힙)
: 주로 완전이진트리 기반으로 구현하며 정렬하는 용도의 이진트리이다
-> 마지막 레벨 노드 제외하고는 포화상태인 트리
cf> 힙 구현
: 완전이진트리 기반이기에 연결리스트보다 배열로 구현하는 게 더 적합함
1-1. max heap / min heap
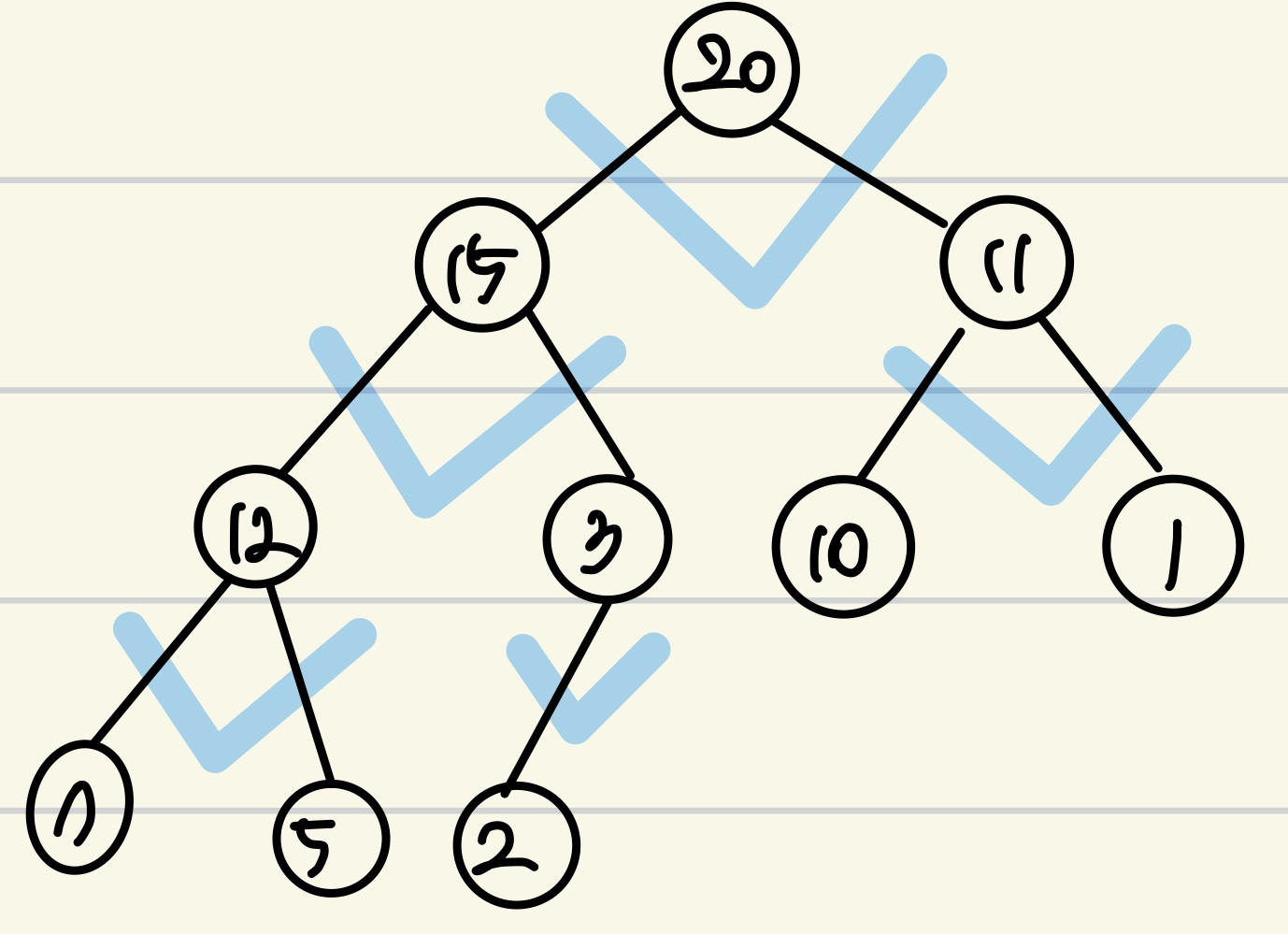
Max heap |
Min heap |
| 부모 노드의 키가 자식 노드들의 키보다 크거나 같은 트리 | 부모 노드의 키가 자식 노드들의 키보다 작거나 같은 트리 |
| 꺼내면 내림차순 정렬 | 꺼내면 오름차순 정렬 |
 |
 |
1-2. 우선순위 큐
: 큐와 유사하지만 우선순위가 높은 아이템이 먼저 처리됨
: max heap과 min heap을 이용하여 우선순위 큐 구현
-> 힙의 key를 우선순위로 사용한다면 힙은 우선순위 큐의 구현체가 된다
1-2-1. 주요 동작
- insert
- delete
- peek
- update ( 부모값보다 크면 insert / 자식값보다 작으면 delete )
1-2-2. 시간 복잡도
우선순위 큐 |
삽입 |
삭제 |
| 리스트 | O(1) | O(N) |
| 힙 | O(logN) | O(logN) |
1-2-3. 구현 (while구문)
#max heap 구현
class HeapQ:
def __init__(self, size):
self.heap=[0] * (size+1)
self.nodeCount=0
self.size = size
def InsertNode(self, item):
if(self.nodeCount ==self.size):
return 'Full'
else:
self.nodeCount+=1
self.heap[self.nodeCount]= item
idx = self.nodeCount
while(idx!=1 and self.heap[idx//2] < self.heap[idx]):
self.heap[idx], self.heap[idx//2]= self.heap[idx//2], self.heap[idx]
idx//=2
def DeleteNode(self):
if(self.nodeCount==0):
return 'Empty'
else:
item = self.heap[1]
self.heap[1]= self.heap[self.nodeCount]
self.nodeCount-=1
idx =1
while(idx*2<=self.nodeCount and self.heap[idx*2]> self.heap[idx]):
child = idx*2
if(self.heap[child]<self.heap[child+1]):
child+=1
self.heap[child], self.heap[idx] = self.heap[idx],self.heap[child]
idx= child
return item
def main():
Priority_Q = HeapQ(10)
Priority_Q.InsertNode(3)
Priority_Q.InsertNode(4)
Priority_Q.InsertNode(1)
Priority_Q.InsertNode(8)
Priority_Q.InsertNode(2)
Priority_Q.InsertNode(9)
print(Priority_Q.DeleteNode())
print(Priority_Q.DeleteNode())
print(Priority_Q.DeleteNode())
print(Priority_Q.DeleteNode())
print(Priority_Q.DeleteNode())
print(Priority_Q.DeleteNode())
if __name__=="__main__":
main()
1-2-4. 구현 (recursive 구문)
class MaxHeap:
def __init__(self):
self.data=[None]
def insert(self,item):
self.data.append(item)
idx = len(self.data)-1
while(idx!=1 and item > self.data[idx//2]):
self.data[idx],self.data[idx//2]=self.data[idx//2],self.data[idx]
idx//=2
def delete(self):
if(len(self.data)>1):
self.data[1],self.data[-1]=self.data[-1], self.data[1]
data= self.data.pop(-1)
self.maxHeapify(1)
else:
data=None
return data
def maxHeapify(self,i):
left = i*2
right = i*2+1
smallest =i
if(left<=len(self.data)-1 and self.data[left]>self.data[smallest]):
smallest =left
if(right<=len(self.data)-1 and self.data[right]>self.data[smallest]):
smallest = right
if(smallest!=i):
self.data[smallest], self.data[i]= self.data[i],self.data[smallest]
self.maxHeapify(smallest)'Python > 자료구조' 카테고리의 다른 글
| [python] LinkedList-bubble sort (0) | 2024.03.27 |
|---|---|
| [python] 이진트리 / 이진 탐색트리(+백준 5639) (1) | 2023.11.21 |
| [python] dummy node 활용한 Linked List (0) | 2023.11.14 |


