1. 이진트리
- 모든 노드의 차수가 <=2 인 트리
- 트리 안의 모든 서브트리는 이진트리
- 모든 노드는 왼쪽 자식 노드와 오른쪽 자식 노드 존재 ( 공백노드도 노드 )
1-1. 이진트리의 넓이 우선 순회 (BFS ; Breadth First Traversal)
class ArrayQueue:
def __init__(self):
self.data = []
def size(self):
return len(self.data)
def isEmpty(self):
return self.size() == 0
def enqueue(self, item):
self.data.append(item)
def dequeue(self):
return self.data.pop(0)
def peek(self):
return self.data[0]
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
class BinaryTree:
def __init__(self, r):
self.root = r
def bft(self):
if(self.root==None):
return []
else:
traverse=[]
queue = ArrayQueue()
queue.enqueue(self.root)
while(not queue.isEmpty()):
now= queue.dequeue()
traverse.append(now.data)
if(now.left):
queue.enqueue(now.left)
if(now.right):
queue.enqueue(now.right)
return traverse
2. 이진 탐색 트리

→ 모든 노드에 대해서,
왼쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 작고
오른쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 큰 성질을 만족하는 이진트리
(모든 원소는 서로 다른 유일한 키를 갖는다)
2-1. BST의 ADT
- insert(key,data) : 트리에 주어진 데이터 원소 추가
- remove(key) : 특정 원소를 트리로부터 삭제
- lookup(key) : 특정 원소 검색
- inorder() : 키의 순서대로 데이터 원소 나열
- min(), max() : 최소 키, 최대 키 가지는 원소 각각 탐색
2-1-1. BST 구현
class Node:
def __init__(self,key,data):
self.key = key
self.data = data
self.left =None
self.right = None
def inorder(self):
traversal=[]
if self.left:
traversal+=self.left.inorder()
traversal.append(self)
if(self.right):
traversal+=self.right.inorder()
return traversal
def min(self):
if(self.left):
return self.left.min()
else:
return self
def max(self):
if(self.right):
return self.right.max()
else:
return self
def lookup(self,key,parent=None):
if(key<self.key):
if(self.left):
return self.left.lookup(key,self)
else:
return None,None
elif(key>self.key):
if(self.right):
return self.right.lookup(key,self)
else:
return None,None
else:
return self,parent
def insert(self,key,data):
if(key<self.key):
if(self.left):
self.left.insert(key,data)
else:
self.left = Node(key,data)
elif(key>self.key):
if(self.right):
self.right.insert(key,data)
else:
self.right = Node(key,data)
else:
raise KeyError
def countChildren(self):
count=0
if(self.left):
count+=1
if(self.right):
count+=1
return count
class BinSearchTree:
def __init__(self):
self.root = None
def inorder(self):
if(self.root):
return self.root.inorder()
else:
return []
def min(self):
if(self.root):
return self.root.min()
else:
return None
def max(self):
if(self.root):
return self.root.max()
else:
return None
def lookup(self,key):
if(self.root):
return self.root.lookup(key)
else:
return None,None
def insert(self,key,data):
if(self.root):
self.root.insert(key,data)
else:
self.root=Node(key,data)
def remove(self,key):
node,parent = self.lookup(key)
if(node):
nChildren = node.countChildren()
if(nChildren==0):
if(parent):
if(parent.left ==node):
parent.left = None
elif(parent.right ==node):
parent.right = None
else:
self.root = None
elif(nChildren==1):
if(node.left):
child= node.left
elif(node.right):
child = node.right
if(parent):
if(parent.left==node):
parent.left = child
elif(parent.right ==node):
parent.right = child
else:
self.root = child
else:
succ_parent=node
succ= node.left
while(succ.right):
succ_parent = succ
succ= succ.right
node.key = succ.key
node.data = succ.data
#처음부터 왼쪽 자식이 없는 경우
if(succ_parent.left == succ):
succ_parent.left = succ.left
else:
succ_parent.right = succ.left
return True
else:
return False
import sys
input = sys.stdin.readline
class Node():
def __init__(self,item):
self.data =item
self.left = None
self.right = None
def traverse(self):
if(self.left):
self.left.traverse()
print(self.data, end=" ")
if(self.right):
self.right.traverse()
def insert(self, item):
if(item < self.data):
if(self.left):
self.left.insert(item)
else:
self.left = Node(item)
elif(item>self.data):
if(self.right):
self.right.insert(item)
else:
self.right=Node(item)
else:
raise IndexError
def search(self,item,parent=None):
if(item<self.data):
if(self.left):
return self.left.search(item,self)
else:
print('Not Exist')
return None,None
elif(item>self.data):
if(self.right):
return self.right.search(item,self)
else:
print('Not Exist')
return None,None
else:
print('exist')
return self,parent
def delete(self, item):
delNode, parent = self.search(item)
if(delNode):
if(parent==None):
self=None
else:
if(delNode.left ==None and delNode.right==None):
if(parent.left==delNode):
parent.left = None
elif(parent.right==delNode):
parent.right = None
elif(delNode.left!=None and delNode.right!=None):
succ_parent = delNode
succ= delNode.right
while(succ.left):
succ_parent = succ
succ=succ.left
delNode.data= succ.data
if(succ_parent.right==succ):
succ_parent.right = succ.right
else:
succ_parent.left = succ.right
else:
if(delNode.left):
child = delNode.left
elif(delNode.right):
child = delNode.right
if(parent==None):
self.root = child
else:
if(parent.left==delNode):
parent.left = child
else:
parent.right = child
else:
print('Node is not exist')
class BinaryTree():
def __init__(self):
self.root = None
def PrintTree(self):
if(self.root):
self.root.traverse()
else:
print('Empty Tree')
def insert(self, item):
if(self.root):
self.root.insert(item)
else:
self.root=Node(item)
def search(self,item):
if(self.root):
return self.root.search(item=item)
else:
print('Empty Tree')
def delete(self, item):
if(self.root):
self.root.delete(item)
else:
print('Empty tree')
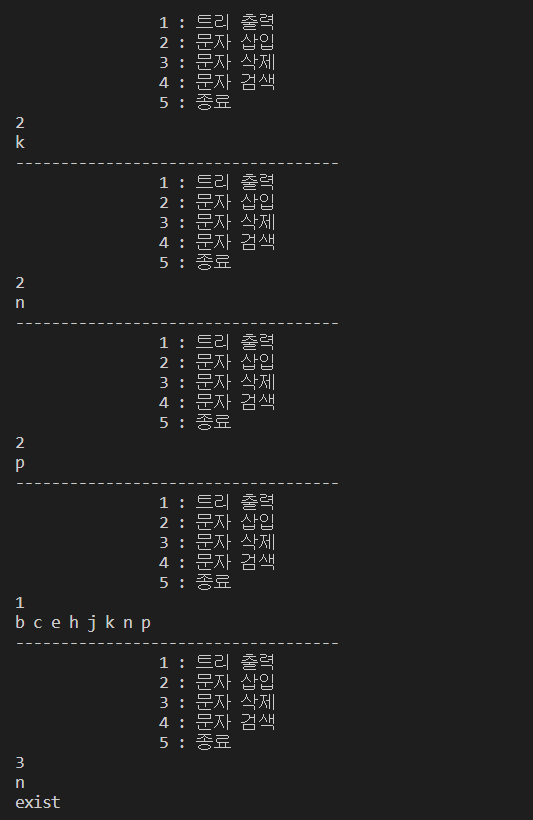
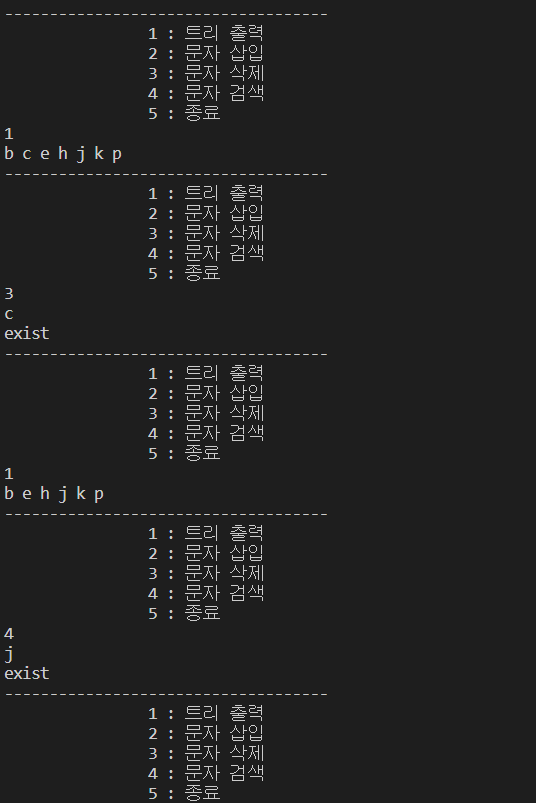
def main():
BST= BinaryTree()
while(True):
print("------------------------------------")
print("\t\t1 : 트리 출력")
print("\t\t2 : 문자 삽입")
print("\t\t3 : 문자 삭제")
print("\t\t4 : 문자 검색")
print('\t\t5 : 종료')
ans = int(input())
if(ans==1):
BST.PrintTree()
print()
elif(ans==2):
item = input().rstrip()
BST.insert(item)
elif(ans==3):
item = input().rstrip()
BST.delete(item)
elif(ans==4):
item = input().rstrip()
BST.search(item)
else:
break
if __name__=="__main__":
main()
2-2. BST의 시간복잡도
: 삽입,삭제,탐색의 시간 복잡도는 트리의 높이를 h라고 가정했을 때 h에 비례
: 이진 트리가 균형적으로 생성되어 있는 경우 h=log(n) => O(logN)
2-3. 이진 탐색 트리가 효율적이지 못한 경우
: 편향트리인 경우
: 선형탐색과 동일한 시간복잡도를 갖게됨 (=O(N))
↓
높이의 균형을 유지함으로써 O(logN)의 탐색 복잡도 보장하는 AVL트리/Red-Black Tree 존재
(추후에 다룰 예정)
2-4. 백준 5639 (이진 탐색 트리 문제)
https://www.acmicpc.net/problem/5639
5639번: 이진 검색 트리
트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다
www.acmicpc.net
2-4-1. 구현
import sys
sys.setrecursionlimit(10**5)
#input은 EOF를 받을 때 EOFError
#sys.stdin.readline은 EOF를 받을 때 빈문자열 리턴
#위 코드로 입력 받으면 입력 후 엔터가 줄 바꿈 기호로 입력됨
input = sys.stdin.readline
class Node():
def __init__(self,item):
self.data = item
self.left = None
self.right = None
def postorder(self):
if(self.left):
self.left.postorder()
if(self.right):
self.right.postorder()
print(self.data)
def insert(self,item):
if(item<self.data):
if(self.left):
self.left.insert(item)
else:
self.left = Node(item)
elif(item>self.data):
if(self.right):
self.right.insert(item)
else:
self.right = Node(item)
else:
raise IndexError
class BinaryTree():
def __init__(self):
self.root = None
def postorder(self):
if(self.root):
self.root.postorder()
else:
pass
def insert(self,item):
if(self.root):
self.root.insert(item)
else:
newNode = Node(item)
self.root = newNode
def main():
BST = BinaryTree()
while(True):
try:
item = int(input())
BST.insert(item)
except:
break
BST.postorder()
if __name__=="__main__":
main()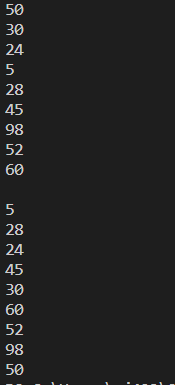
2-4-2. EOFError
: "End of File Error"의 약자로 파일을 읽을 때 파일의 끝을 만나면 발생하는 에러
( 더이상 읽을 내용이 없어서 발생하는 에러 )
- input()은 EOFError 발생시킴
- sys.stdin.readline()은 빈 문자열 반환
=> 엔터 들어올 때까지 입력받게 하고자 한다면, 아래와 같이 코드 작성
#input()
while True:
try:
data= input()
except EOFError:
break#sys.stdin.readline()
import sys
input = sys.stdin.readline
while True:
temp =input()
if temp == "":
break
#참고로 문자열을 int()로 형변환 해주면 개행문자는 사라지고 정수형태만 남는다
cf> [파이썬 에러] ValueError: invalid literal for int() with base 10
-> 구현 부분에서 try-exception 처리 안하면 발생하는 에러 ( 빈 문자열 int로 변환하는 것이기에)
-> 파이썬에서 데이터 형 변환 시 발생하는 에러
-> input으로 받은 값이 실수 문자형일 경우 int() 함수가 받을 값이 아니기에 float형으로 변환 후 int()함수 사용해야함
| int() | 정수 형태의 문자열 (str ➝ int) |
| 실수 값 (float ➝ int) | |
| float() | 실수/정수 형태의 문자열/정수 (str/int ➝ float) |
| str() | 정수/실수 값 (int/float ➝ str) |
'Python > 자료구조' 카테고리의 다른 글
| [python] LinkedList-bubble sort (0) | 2024.03.27 |
|---|---|
| [python] 우선순위 큐 (3) | 2023.11.20 |
| [python] dummy node 활용한 Linked List (0) | 2023.11.14 |


