1. 균형이진탐색트리 (Adelson-Velskii&Landis)
: 균형인수(Balance Factor:BF)를 이용하여 트리가 비균형 상태로 되면 스스로 노드들을 재배치하여 균형 상태를 유지하도록 하는 트리
: 평균, 최선, 최악 시간복잡도 : O(log(n))
: 모든 노드의 BF가 ±1이하이면 AVL트리라고 할 수 있음
cf. AVL의 자세한 동작은 아래 사이트에서 알 수 있음
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
AVL Tree Visualzation
www.cs.usfca.edu
1-1. 해당 트리 구성하는 동작
- 높이
- 균형 인수(BF)
- RR/LL/RL/LR 유형에 따른 rotation (=rebalancing)
- 노드 삽입
- 노드 삭제
(1) 높이
int getHeight(TreeNode* node) {
if (node == NULL) {
return 0;
}
else {
return max(getHeight(node->left), getHeight(node->right)) + 1;
}
}
(2) BF
: Height(Left SubTree) - Height(Right SubTree)

int getBF(TreeNode* node) {
return getHeight(node->left) - getHeight(node->right);
}
(3) Types of unbalancing of BF
- RR
- LL
- LR
- RL

TreeNode* Type_RR(TreeNode** root) {
TreeNode* child = (*root)->right;
(*root)->right = child->left;
child->left = (*root);
return child;
}TreeNode* Type_LL(TreeNode** root) {
TreeNode* child = (*root)->left;
(*root)->left = child->right;
child->right = (*root);
return child;
}
TreeNode* Type_LR(TreeNode** root) {
(*root)->left = Type_RR(&((*root)->left));
return Type_LL(root);
}TreeNode* Type_RL(TreeNode** root) {
(*root)->right = Type_LL(&((*root)->right));
return Type_RR(root);
}
(4) Insert

TreeNode* insert(TreeNode** node, int key) {
//맨 처음으로 노드를 삽입하는 경우
if (root==NULL) {
root = new TreeNode(key);
return NULL;
}
if (*node == NULL) {
return new TreeNode(key);
}
if ((*node)->key >key) {
(*node)->left = insert(&((*node)->left), key);
*node = rebalance(node);
}
else {
(*node)->right = insert(&((*node)->right), key);
*node = rebalance(node);
}
return *node;
}
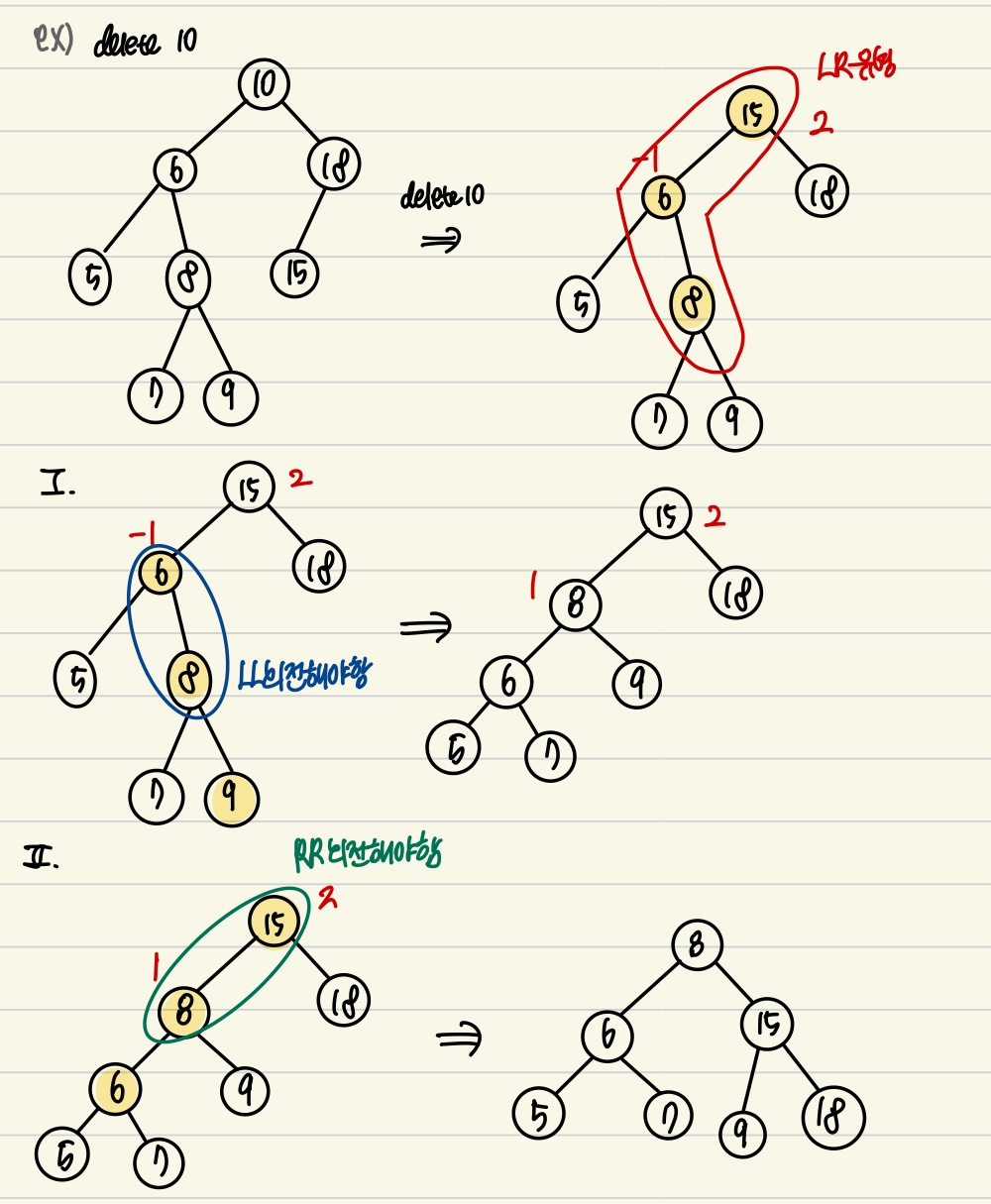
(5) Delete
- BST 삭제연산 함수
- BST 삭제연산 함수를 하고 rebalancing 해주는 AVL 삭제연산 함수
cf. 어떤 특정 key를 갖는 노드를 삭제하고 난 후의 rebalancing을 해줘야 하는 가능성을 가진 노드는 해당 노드의 조상 노드들이다
→ true를 반환하면 BST delete연산을 수행한 후 rebalancing 과정을 거치고 false를 반환하여 더이상 부모 노드 제외한 조상노드들인 경우엔 BST delete연산을 하지않고 rebalancing과정만 거치도록 함
AVL.hbool trim(TreeNode** node, int key) { if ((*node)->key == key) { return true; } if ((*node)->key > key) { if (trim(&((*node)->left), key)==true) { BST_delete(&root, key); } } else if ((*node)->key < key) { if (trim(&((*node)->right), key)==true) { BST_delete(&root, key); } } *node = rebalance(node); return false; }
main.cpp
void BST_delete(TreeNode ** tr, int key) { TreeNode* curNode = *tr; TreeNode* preNode = NULL; while (curNode != NULL) { if (curNode->key == key) { break; } else if (curNode->key < key) { preNode = curNode; curNode = curNode->right; } else if (curNode->key > key) { preNode = curNode; curNode = curNode->left; } } if (curNode == NULL) { cout << "삭제할 노드 존재하지 않습니다\n"; return; } if (curNode->left == NULL && curNode->right == NULL) { if (preNode->right == curNode) { preNode->right = NULL; } else if (preNode->left == curNode) { preNode->left = NULL; } delete curNode; curNode= NULL; } else if (curNode->left != NULL && curNode->right != NULL) { TreeNode* succ = curNode; TreeNode* pre_succ = curNode; succ = succ->left; while (succ->right != NULL) { pre_succ = succ; succ = succ->right; } curNode->key = succ->key; if (pre_succ->left == succ) { pre_succ->left = succ->left; } else { pre_succ->right = succ->left; } } else { TreeNode* child=NULL; if (preNode != NULL) { if (curNode->left != NULL) { child = curNode->left; } else if (curNode->right != NULL) { child = curNode->right; } if (preNode->left == curNode) { preNode->left = child; } else { preNode->right = child; } }else{ *tr = child; } } }
1-2. 전체 소스코드
AVL.h
#pragma once #include <iostream> using namespace std; class TreeNode { private: int key; TreeNode* left; TreeNode* right; public: TreeNode(int item): key(item), left(NULL),right(NULL){} int getHeight(TreeNode* node) { if (node == NULL) { return 0; } else { return max(getHeight(node->left), getHeight(node->right)) + 1; } } int getBF(TreeNode* node) { return getHeight(node->left) - getHeight(node->right); } TreeNode* Type_LL(TreeNode** root) { TreeNode* child = (*root)->left; (*root)->left = child->right; child->right = (*root); return child; } TreeNode* Type_RR(TreeNode** root) { TreeNode* child = (*root)->right; (*root)->right = child->left; child->left = (*root); return child; } TreeNode* Type_LR(TreeNode** root) { (*root)->left = Type_RR(&((*root)->left)); return Type_LL(root); } TreeNode* Type_RL(TreeNode** root) { (*root)->right = Type_LL(&((*root)->right)); return Type_RR(root); } friend void BST_delete(TreeNode** tr, int key); friend class AVLTree; }; class AVLTree { private: TreeNode* root; public: AVLTree():root(NULL){} AVLTree(TreeNode * item):root(item){} void setRoot(TreeNode* item) { root = item; } TreeNode** getRootPointer() { return &root; } TreeNode* getRoot() { return root; } TreeNode* rebalance(TreeNode** node) { int BF = (*node)->getBF((*node)); if (BF == 2) { if ((*node)->left->getBF((*node)->left) >= 0) { //LL유형 *node = (*node)->Type_LL(node); } else { *node = (*node)->Type_LR(node); } } else if(BF==-2) { if ((*node)->right->getBF((*node)->right) <= 0) { //LL유형 *node = (*node)->Type_RR(node); } else { *node = (*node)->Type_RL(node); } } return *node; } TreeNode* insert(TreeNode** node, int key) { //맨 처음으로 노드를 삽입하는 경우 if (root==NULL) { root = new TreeNode(key); return NULL; } if (*node == NULL) { return new TreeNode(key); } if ((*node)->key >key) { (*node)->left = insert(&((*node)->left), key); *node = rebalance(node); } else { (*node)->right = insert(&((*node)->right), key); *node = rebalance(node); } return *node; } bool trim(TreeNode** node, int key) { if ((*node)->key == key) { return true; } if ((*node)->key > key) { if (trim(&((*node)->left), key)==true) { BST_delete(&root, key); *node = rebalance(node); } } else if ((*node)->key < key) { if (trim(&((*node)->right), key)==true) { BST_delete(&root, key); *node = rebalance(node); } } return false; } void LVR(TreeNode* node) { if (node == NULL) { return; } LVR(node->left); cout << node->key << " "; LVR(node->right); } };
main.cpp
#include "AVL.h" #include <iostream> using namespace std; void BST_delete(TreeNode ** tr, int key) { TreeNode* curNode = *tr; TreeNode* preNode = NULL; while (curNode != NULL) { if (curNode->key == key) { break; } else if (curNode->key < key) { preNode = curNode; curNode = curNode->right; } else if (curNode->key > key) { preNode = curNode; curNode = curNode->left; } } if (curNode == NULL) { cout << "삭제할 노드 존재하지 않습니다\n"; return; } if (curNode->left == NULL && curNode->right == NULL) { if (preNode->right == curNode) { preNode->right = NULL; } else if (preNode->left == curNode) { preNode->left = NULL; } delete curNode; curNode= NULL; } else if (curNode->left != NULL && curNode->right != NULL) { TreeNode* succ = curNode; TreeNode* pre_succ = curNode; succ = succ->left; while (succ->right != NULL) { pre_succ = succ; succ = succ->right; } curNode->key = succ->key; if (pre_succ->left == succ) { pre_succ->left = succ->left; } else { pre_succ->right = succ->left; } } else { TreeNode* child=NULL; if (preNode != NULL) { if (curNode->left != NULL) { child = curNode->left; } else if (curNode->right != NULL) { child = curNode->right; } if (preNode->left == curNode) { preNode->left = child; } else { preNode->right = child; } }else{ *tr = child; } } } int main() { AVLTree avl; cout << "*******AVL 트리 삽입********\n"; avl.insert(avl.getRootPointer(), 50); avl.insert(avl.getRootPointer(), 20); avl.insert(avl.getRootPointer(), 60); avl.insert(avl.getRootPointer(), 10); avl.insert(avl.getRootPointer(), 8); avl.insert(avl.getRootPointer(), 15); avl.insert(avl.getRootPointer(), 32); avl.insert(avl.getRootPointer(), 46); avl.insert(avl.getRootPointer(), 11); avl.insert(avl.getRootPointer(), 48); avl.LVR(avl.getRoot()); cout << "\n*******AVL 트리 원소 중 60 삭제***********\n"; avl.trim(avl.getRootPointer(), 60); avl.LVR(avl.getRoot()); cout << "\n*******AVL 트리 원소 중 32 삭제***********\n"; avl.trim(avl.getRootPointer(), 32); avl.LVR(avl.getRoot()); getchar(); return 0; }
| {50, 20, 60, 10, 8, 15, 32, 46, 11, 48} 순차적으로 삽입 | |
| BST Tree | AVL Tree |
 |
 |
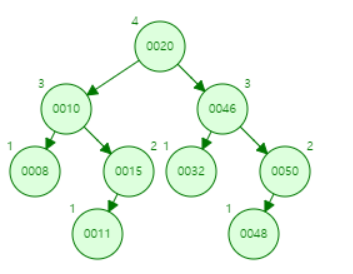
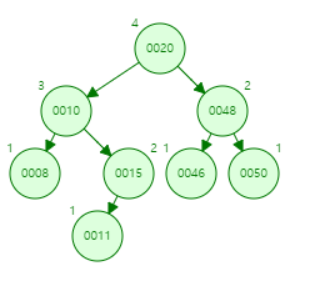
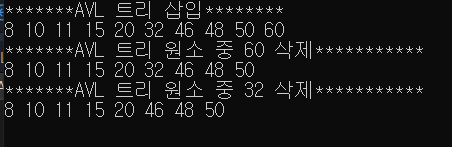
(1번째 사진) 60 삭제하고 난 후 AVL트리
(2번째 사진) 32 삭제하고 난 후 AVL트리
(3번째 사진) 구현 결과 출력
'C++ > 자료구조' 카테고리의 다른 글
| [c++] Heap (1) | 2023.12.08 |
|---|---|
| [C++]Reverse doubly linked list with sentinel nodes (0) | 2023.11.29 |
| [C++]Doubly linked list with sentinel nodes (1) | 2023.11.29 |
| [c++] 스택 활용한 수식 계산 (0) | 2023.11.16 |
| [C++]원형큐 (0) | 2023.11.14 |



