1. 힙
: 관련 내용은 아래 글 참조
2023.11.20 - [Python/자료구조] - [python] 우선순위 큐
[python] 우선순위 큐
1. Heap(힙) : 주로 완전이진트리 기반으로 구현하며 정렬하는 용도의 이진트리이다 -> 마지막 레벨 노드 제외하고는 포화상태인 트리 cf> 힙 구현 : 완전이진트리 기반이기에 연결리스트보다 배열
growingupis.tistory.com
1-1. 힙 기본 동작 구성
- swim_up : 특정 인덱스에서 위로 올라가며 조건 만족하면 swap
- sink_down : 특정 인덱스에서 아래로 내려가며 조건 만족하면 swap
- trim : 힙의 루트노드 반환
- grow : 힙에 원소 삽입
- swap : 노드 교환
Heap.h
#pragma once #include <iostream> using namespace std; //MaxHeap구현 class Heap { private: int* data; int capacity; //최대 존재할 수 있는 노드의 개수 int n; //힙에 존재하는 노드의 개수 public: Heap(int num) : data(new int[num]), capacity(num), n(0) {} void setData(int* item) { data = item; } void setCapacity(int item) { capacity = item; } void setN(int item) { n = item; } int getSize() { return n; } void swim_up(int idx) { while (idx != 1 && data[idx] > data[idx / 2]) { swap(idx, idx / 2); idx /= 2; } } void sink_down(int idx) { while (idx * 2 <= n && data[idx] < data[idx * 2]) { int child = idx * 2; if (data[child + 1] > data[child]) { child++; } swap(idx, child); idx = child; } } void grow(int item) { if (isFull()) { cout << "더이상 삽입할 수 없습니다\n"; return; } else { data[++n] = item; swim_up(n); } } int trim() { if (isEmpty()) { cout << "삭제할 노드가 존재하지 않습니다\n"; return 0; } else { int item = data[1]; data[1] = data[n]; n--; sink_down(1); return item; } } void swap(int a, int b) { int temp = data[a]; data[a] = data[b]; data[b] = temp; } int isFull() { return capacity == n; } int isEmpty() { return n == 0; } void PrintHeap() { for (int i = 1; i <= n; i++) { cout << data[i] << " "; } cout << endl; } };
main.cpp
#include "Heap.h" #include <iostream> using namespace std; int main() { Heap heap(10); heap.grow(8); heap.grow(7); heap.grow(3); heap.grow(6); heap.grow(1); heap.grow(4); cout << "*****힙 출력******" << endl; heap.PrintHeap(); cout << "*****힙 내림차순 정렬******" << endl; int size = heap.getSize(); for (int i = 0; i < size; i++) { cout << heap.trim() << " "; } cout << endl; getchar(); return 0; }

1-2. 힙 정렬
: max heap / min heap을 이용하여 오름차순 / 내림차순 정렬을 하는 알고리즘
ex. 오름차순 정렬
- 기존 완전 이진트리를 ToHeap함수를 통해 인덱싱하여 1부터 시작하도록 힙구현의 베이스 마련
- Heapify 함수를 통해 max heap으로 구성시킴
- 힙을 구성하는 노드의 개수만큼 반복문을 돌리며 1번째 원소 마지막 원소의 위치를 바꾸어가며 오름차순으로 정렬되도록함
(1) ToHeap
ex. int arr[5]={1,2,3,4,5}
→ {0,1,2,3,4,5}로 힙구현에 용이하도록 바꾼다
template <typename T>
Heap<T>* ToHeap(T* data, int size) {
Heap<T>* heap = new Heap<T>(MAX_SIZE);
heap->setN(size);
for (int i = 0; i < size; i++) {
heap->getData()[i + 1] = data[i];
}
return heap;
}
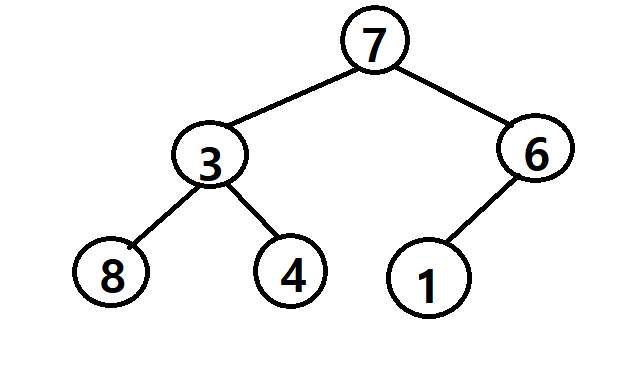
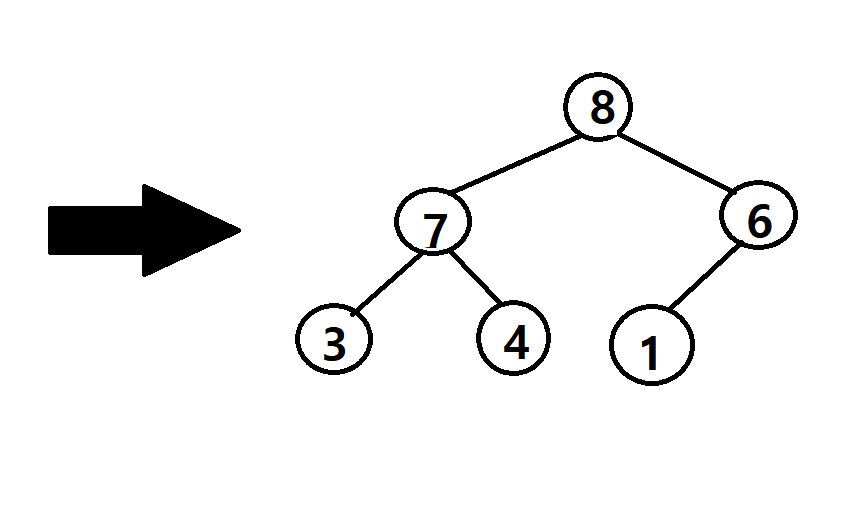
(2) Heapify
: Leaf Node는 제외하고 Internal node에 대해서만 sink_down 동작을 통해 max heap으로 바꿈
: 이때, 마지막 internal node의 인덱스 = 트리의 전체 노드 개수 / 2
void Heapify() {
int last_internal = n / 2;
for (int i = last_internal; i >= 1; i--) {
sink_down(i);
}
}
(3) Sorting

cf. 이때 오름차순으로 정렬하려면 그냥 min heap으로 만들어서 계속 delete하면 되지않나 생각했었음
: delete할 때마다 루트 노드들은 마지막 노드의 값으로 덮어쓰여지기에 트리에 존재하지 않게 됨
: 따라서, max heap으로 만든뒤 루트노드와 마지막 노드를 swap하고 그 루트노드에 대해서 sink_down을 해나가는 과정이 모든 데이터들을 보존하면서 정렬할 수 있음(이때, 다 수행하고 난 뒤에 힙의 노드의 개수 다시 재조정해주어야함)
1) 동작 과정
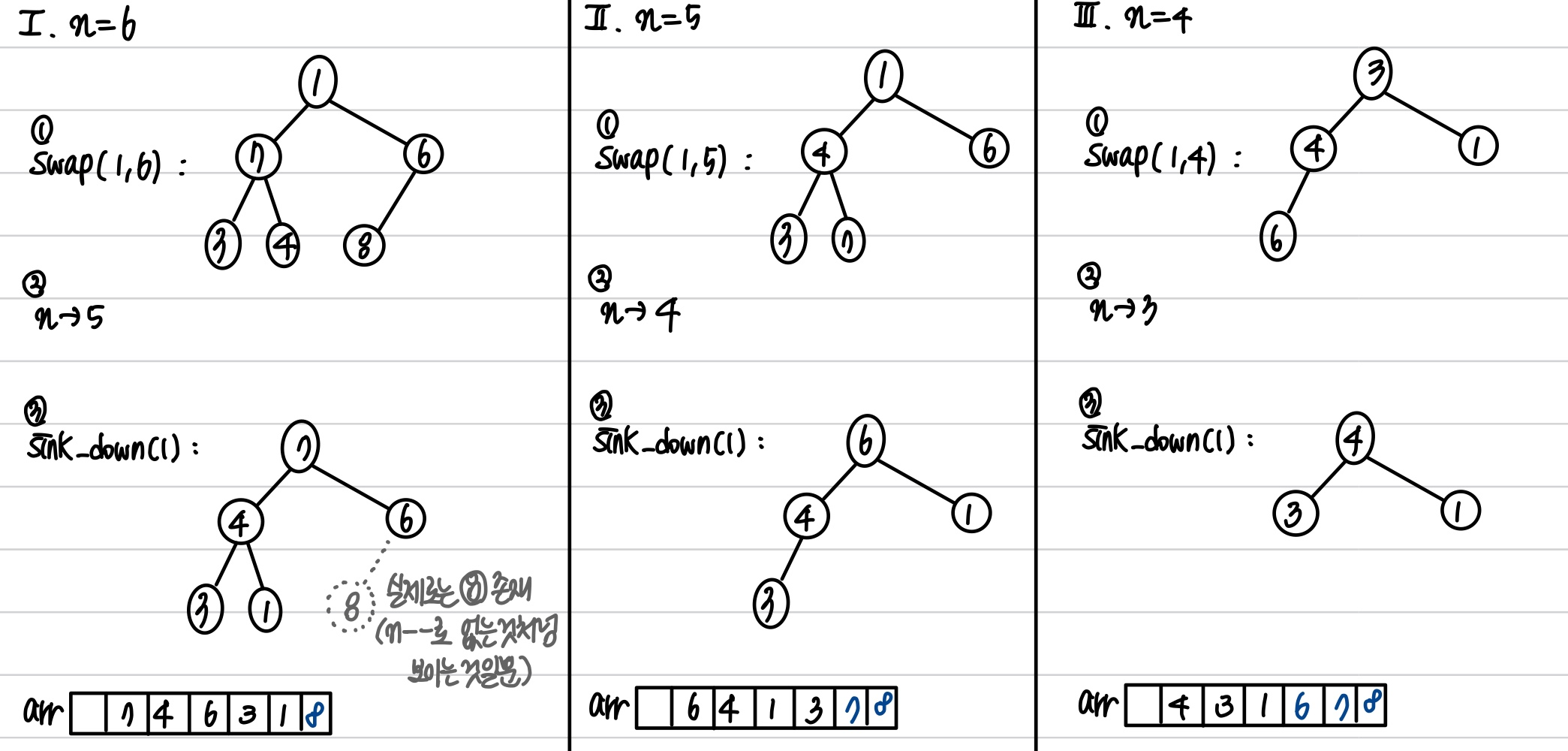
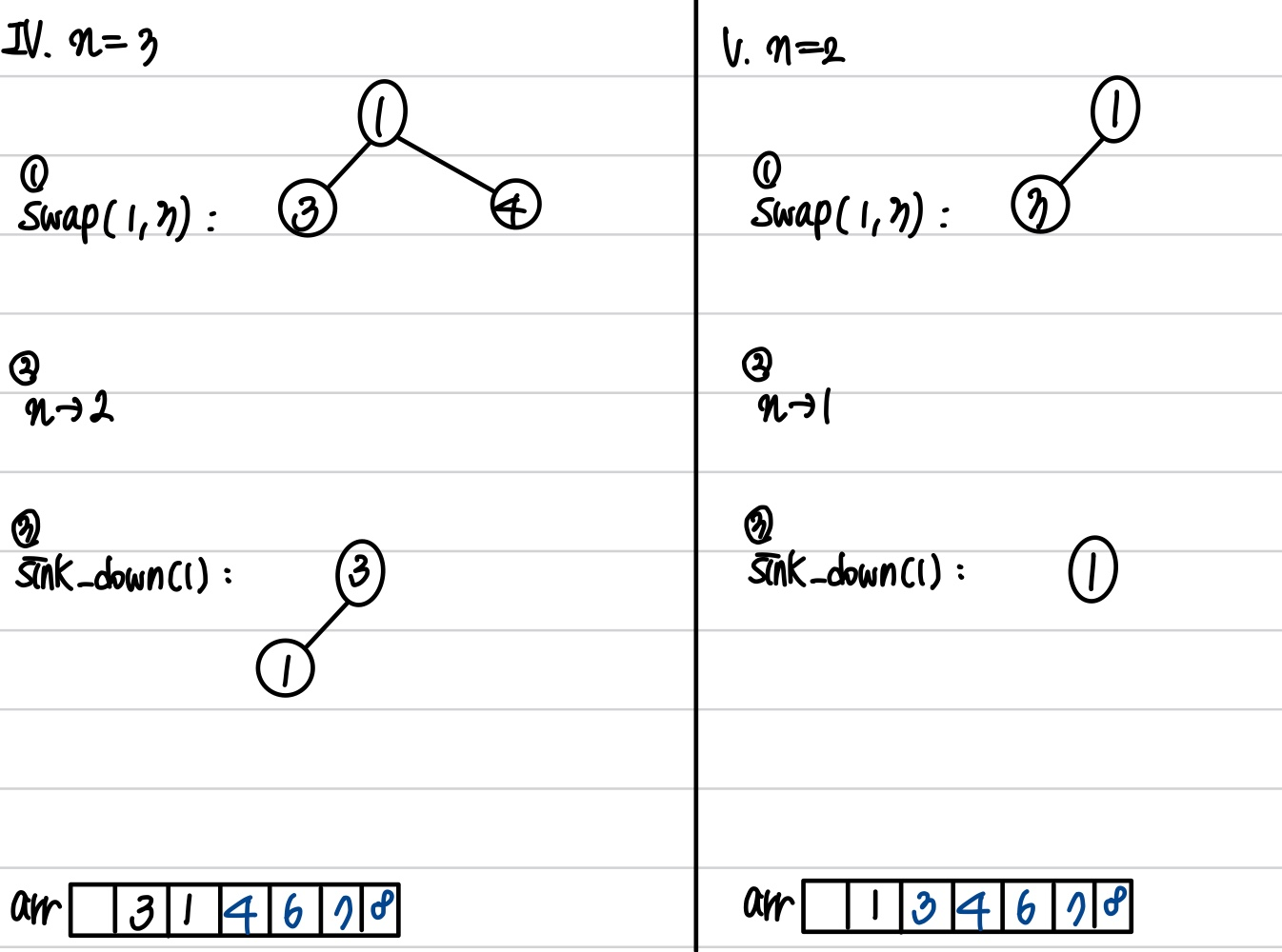
int size = NewHeap->getSize();
for (int i = 1; i <= size; i++) {
NewHeap->swap(1, NewHeap->getSize());
NewHeap->DownNum();
NewHeap->sink_down(1);
NewHeap->PrintHeap();
}
NewHeap->setN(size);
1-2-1. 전체 소스코드
Heap.h
#pragma once #pragma once #include <iostream> using namespace std; #define MAX_SIZE 30 //MaxHeap구현 template <typename T> class Heap { private: T* data; int capacity; //최대 존재할 수 있는 노드의 개수 int n; //힙에 존재하는 노드의 개수 public: Heap(int num) : data(new T[num]), capacity(num), n(0) {} T* getData() { return data; } void DownNum() { n--; } void setCapacity(int item) { capacity = item; } void setN(int item) { n = item; } int getSize() { return n; } void swim_up(int idx) { while (idx != 1 && data[idx] > data[idx / 2]) { swap(idx, idx / 2); idx /= 2; } } void sink_down(int idx) { while (idx * 2 <= n && data[idx] < data[idx * 2]) { int child = idx * 2; if (child+1<=n && data[child + 1] > data[child]) { child++; } swap(idx, child); idx = child; } } void grow(T item) { if (isFull()) { cout << "더이상 삽입할 수 없습니다\n"; return; } else { data[++n] = item; swim_up(n); } } T trim() { if (isEmpty()) { cout << "삭제할 노드가 존재하지 않습니다\n"; return 0; } else { T item = data[1]; data[1] = data[n]; n--; sink_down(1); return item; } } void swap(int a, int b) { T temp = data[a]; data[a] = data[b]; data[b] = temp; } int isFull() { return capacity == n; } int isEmpty() { return n == 0; } void PrintHeap() { for (int i = 1; i <= n; i++) { cout << data[i] << " "; } cout << endl; } void Heapify() { int last_internal = n / 2; for (int i = last_internal; i >= 1; i--) { sink_down(i); } } };
main.cpp
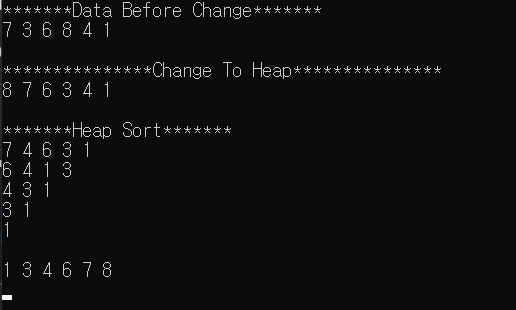
#include <iostream> using namespace std; #include "Heap.h" #define MAX_SIZE 30 template <typename T> Heap<T>* ToHeap(T* data, int size) { Heap<T>* heap = new Heap<T>(MAX_SIZE); heap->setN(size); for (int i = 0; i < size; i++) { heap->getData()[i + 1] = data[i]; } return heap; } int main() { int data[] = {7,3,6,8,4,1 }; Heap<int>* NewHeap = ToHeap<int>(data, sizeof(data) / sizeof(int)); cout << "*******Data Before Change*******\n"; NewHeap->PrintHeap(); cout << "\n***************Change To Heap***************\n"; NewHeap->Heapify(); NewHeap->PrintHeap(); // cout << "\n*******Heap Sort*******\n"; int size = NewHeap->getSize(); for (int i = 1; i <= size; i++) { NewHeap->swap(1, NewHeap->getSize()); NewHeap->DownNum(); NewHeap->sink_down(1); NewHeap->PrintHeap(); } NewHeap->setN(size); NewHeap->PrintHeap(); getchar(); return 0; }

'C++ > 자료구조' 카테고리의 다른 글
| [C++]AVL Tree (0) | 2023.12.07 |
|---|---|
| [C++]Reverse doubly linked list with sentinel nodes (0) | 2023.11.29 |
| [C++]Doubly linked list with sentinel nodes (1) | 2023.11.29 |
| [c++] 스택 활용한 수식 계산 (0) | 2023.11.16 |
| [C++]원형큐 (1) | 2023.11.14 |



